题目内容
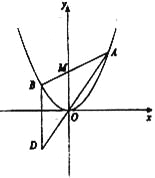
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析, ![]() .
.
【解析】试题分析:(1)由题意设![]() ,运用两直线垂直的条件:斜率之积为
,运用两直线垂直的条件:斜率之积为![]() ,解得
,解得![]() ,再由两点的距离公式可得半径,进而得到所求圆的标准方程;(2)(i)设直线
,再由两点的距离公式可得半径,进而得到所求圆的标准方程;(2)(i)设直线![]() 的方程为
的方程为![]() ,联立圆的方程,可得
,联立圆的方程,可得![]() 的二次方程,运用韦达定理,即可证得
的二次方程,运用韦达定理,即可证得![]() 为定值;(ii)由两点的距离公式,以及韦达定理和基本不等式,化简整理,即可得到所求最大值.
为定值;(ii)由两点的距离公式,以及韦达定理和基本不等式,化简整理,即可得到所求最大值.
试题解析:(1)设圆心![]() 的坐标为
的坐标为![]() ,则
,则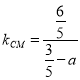 ,又
,又![]() ,
,
由题意可知, ![]() ,则
,则![]() ,
,
故![]() ,所以
,所以![]() ,即半径
,即半径![]() . 故圆
. 故圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
由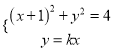 得:
得: ![]() ,
,
所以![]() ,
, ![]() .
.
(ⅰ)![]() 为定值,
为定值,
(ⅱ)![]()
![]()
![]()
![]()
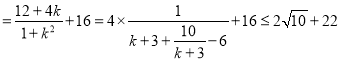
(当且仅当![]() ,即
,即![]() 时等号成立)故
时等号成立)故![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目