题目内容
【题目】已知椭圆![]() 的中心在原点,焦点
的中心在原点,焦点![]() 、
、![]() 在
在![]() 轴上,离心率为
轴上,离心率为![]() ,在椭圆
,在椭圆![]() 上有一动点
上有一动点![]() 与
与![]() 、
、![]() 的距离之和为4,
的距离之和为4,
(Ⅰ) 求椭圆E的方程;
(Ⅱ) 过![]() 、
、![]() 作一个平行四边形,使顶点
作一个平行四边形,使顶点![]() 、
、![]() 、
、![]() 、
、![]() 都在椭圆
都在椭圆![]() 上,如图所示.判断四边形
上,如图所示.判断四边形![]() 能否为菱形,并说明理由.
能否为菱形,并说明理由.

【答案】(1) ![]() (2)
(2) ![]() 不能是菱形
不能是菱形
【解析】试题分析:(1)由椭圆离心率为![]() ,在椭圆E上有一动点A与F1、F2的距离之和为4,列出方程组,求出a=2,b=
,在椭圆E上有一动点A与F1、F2的距离之和为4,列出方程组,求出a=2,b=![]() ,由此能求出椭圆E的方程.(2)由F1(﹣1,0),令直线AB的方程为x=my﹣1,联立方程组
,由此能求出椭圆E的方程.(2)由F1(﹣1,0),令直线AB的方程为x=my﹣1,联立方程组![]() ,得(3m2+4)y2﹣6my﹣9=0,由此利用韦达定理、直线垂直的性质,结合已知条件能求出四边形ABCD不能是菱形.
,得(3m2+4)y2﹣6my﹣9=0,由此利用韦达定理、直线垂直的性质,结合已知条件能求出四边形ABCD不能是菱形.
解析:
(Ⅰ)由条件得![]() 所以
所以![]()
∴椭圆E的方程是![]()
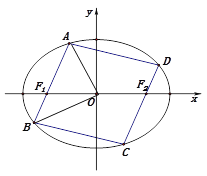
(Ⅱ)因为![]() ,如图,直线
,如图,直线![]() 不能平行于
不能平行于![]() 轴,所以令直线
轴,所以令直线![]() 的方程
的方程
为![]() ,
, ![]() ,
,
联立方程, ![]() ,
,
得![]() ,
,
∴![]() ,
, ![]() .
.
若![]() 是菱形,则
是菱形,则![]() ,
,
即![]() ,
,
于是有![]() ,
,
又![]()
![]() ,
,
所以有![]() ,
,
得到![]() ,
,
显然这个方程没有实数解,故![]() 不能是菱形.
不能是菱形.

练习册系列答案
相关题目
【题目】一次考试中,五名学生的数学、物理成绩如下表
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
(1)要在这五名学生中选2名参加一项活动,求选中的同学中至少有一人的物理成绩高于90分的概率.
(2)求出这些数据的线性回归直线方程.
参考公式回归直线的方程是: ![]() ,
,
其中对应的回归估计值.  ,
, ![]() .
.