题目内容
1.画出函数y=$\frac{1}{2}$sin(2x-$\frac{4π}{3}$)的简图,并指出是如何由y=sinx的图象变换得到的.分析 利用五点法即可作出函数的图象,由函数y=Asin(ωx+φ)的图象变换规律可得解.
解答 用五点作图法作出f(x)的简图.列表:
| 2x-$\frac{4π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{2π}{3}$ | $\frac{11π}{12}$ | $\frac{7π}{6}$ | $\frac{17π}{12}$ | $\frac{5π}{3}$ |
| $\frac{1}{2}$sin(2x-$\frac{4π}{3}$) | 0 | $\frac{1}{2}$ | 0 | -$\frac{1}{2}$ | 0 |
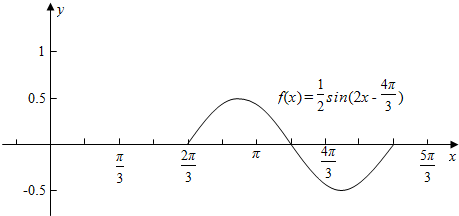
将y=sinx沿着x轴向右平移$\frac{4π}{3}$个答案得到y=sin(x-$\frac{4π}{3}$),然后纵坐标不变,横坐标变为原来的$\frac{1}{2}$,即可得到y=sin(2x-$\frac{4π}{3}$)的图象,然后纵坐标变为原来的$\frac{1}{2}$即可.
点评 本题考查的知识点是五点法作函数y=Asin(ωx+φ)的图象,其中描出五个关键点的坐标是解答本题的关键.

练习册系列答案
相关题目
 已知定义在R函数f(x)满足:f(-x)=-f(x),且当x≤0时,f(x)=x2+2x.
已知定义在R函数f(x)满足:f(-x)=-f(x),且当x≤0时,f(x)=x2+2x.