题目内容
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 存在两个极值点
存在两个极值点![]() ,求证:无论实数
,求证:无论实数![]() 取什么值都有
取什么值都有![]() .
.
【答案】(1)答案见解析; (2)证明过程见解析.
【解析】
试题分析:(1)先求得定义域为![]() ,求导通分后研究导函数的分子,利用判别式对分子根的个数和分布进行分类讨论,由此求得函数的单调区间;(2)由(1)知
,求导通分后研究导函数的分子,利用判别式对分子根的个数和分布进行分类讨论,由此求得函数的单调区间;(2)由(1)知![]() 时有两个极值点,且
时有两个极值点,且![]() ,由此利用差比较法,计算
,由此利用差比较法,计算![]() 的最小值为
的最小值为![]() ,即可得证.
,即可得证.
试题解析:(1)函数的定义域为![]() .
.
![]() ,记
,记![]() ,判别式
,判别式![]() .
.
①当![]() 即
即![]() 时,
时,![]() 恒成立,
恒成立,![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增.
上单调递增.
②当![]() 或
或![]() 时,方程
时,方程![]() 有两个不同的实数根
有两个不同的实数根![]() ,记
,记![]() ,
,![]() ,显然
,显然![]()
(ⅰ)若![]() ,
,![]() 图象的对称轴
图象的对称轴![]() ,
,![]() .
.
两根![]() 在区间
在区间![]() 上,可知当
上,可知当![]() 时函数
时函数![]() 单调递增,
单调递增,![]() ,所以
,所以![]() ,所以
,所以![]() 在区间
在区间![]() 上递增.
上递增.
(ⅱ)若![]() ,则
,则![]() 图象的对称轴
图象的对称轴![]() ,
,![]() .,所以
.,所以![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递减.当
上单调递减.当![]() 或
或![]() 时,
时,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
综上,当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)由(1)知当![]() 时,
时,![]() 没有极值点,当
没有极值点,当![]() 时,
时,![]() 有两个极值点
有两个极值点![]() ,且
,且![]() .
.
![]() ,
,
∴![]() 又
又![]() ,
,
![]() .记
.记![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 时单调递增,
时单调递增,![]() ,所以
,所以![]() ,所以
,所以![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了增强环保意识,某社团从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
优秀 | 非优秀 | 总计 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
(1)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(2)为参加市举办的环保知识竞赛,学校举办预选赛,现在环保测试优秀的同学中选3人参加预选赛,已知在环保测试中优秀的同学通过预选赛的概率为![]() ,若随机变量
,若随机变量![]() 表示这3人中通过预选赛的人数,求
表示这3人中通过预选赛的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:![]() =
=![]()
| 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程![]() ;
;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
(参考公式: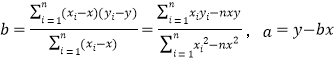 ,).
,).