题目内容
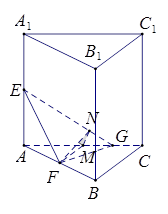
如图,在直三棱柱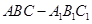 中,
中,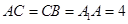 ,
,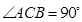 ,
,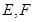 分别是
分别是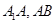 的中点,点
的中点,点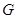 在
在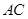 上,且
上,且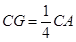 ,则二面角
,则二面角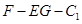 的余弦值为 ;点
的余弦值为 ;点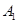 到平面
到平面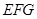 的距离为 。
的距离为 。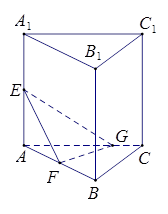
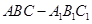 中,
中,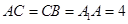 ,
,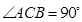 ,
,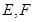 分别是
分别是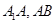 的中点,点
的中点,点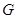 在
在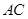 上,且
上,且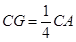 ,则二面角
,则二面角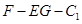 的余弦值为 ;点
的余弦值为 ;点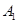 到平面
到平面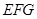 的距离为 。
的距离为 。
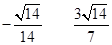
方法一:如图,取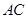 的中点
的中点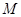 ,连结
,连结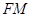 ,则
,则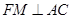 。
。
∵三棱柱 为在直三棱柱,
为在直三棱柱,
∴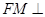 面
面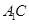 ,∴
,∴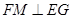 。
。
过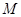 作
作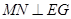 于
于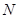 ,连结
,连结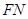 ,则
,则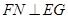 。
。
∴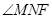 为二面角
为二面角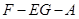 的平面角。
的平面角。
在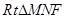 中,
中,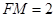 ,
,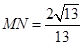 ,则
,则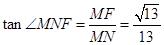 ,得
,得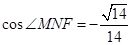 。
。
而二面角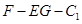 与二面角
与二面角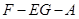 互补,故二面角
互补,故二面角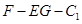 的余弦值为
的余弦值为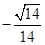 。
。
设点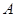 到平面
到平面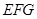 的距离为
的距离为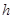 ,由
,由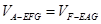 ,得
,得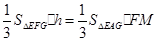 ,即
,即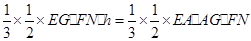 ,∴
,∴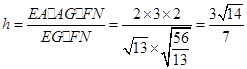 。
。
∵点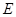 是
是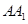 的中点,∴
的中点,∴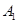 到平面
到平面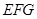 的距离与点
的距离与点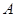 到平面
到平面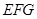 的距离相等,为
的距离相等,为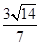 。
。
方法二:建立如图所示直角坐标系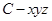 ,则
,则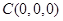 ,
,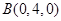 ,
,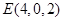 ,
,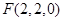 ,
,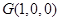 ,
,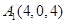 。
。
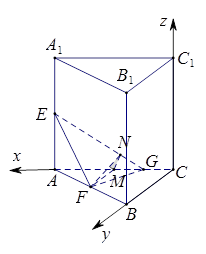
向量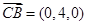 为平面
为平面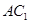 的一个法向量。
的一个法向量。
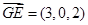 ,
,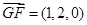 。
。
设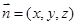 为平面
为平面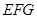 的法向量,则
的法向量,则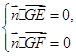 ,即
,即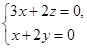 ,取
,取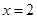 ,得平面
,得平面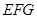 的一个法向量为
的一个法向量为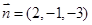 。
。
得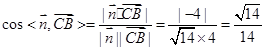 。由图知,二面角
。由图知,二面角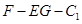 为钝角,故二面角
为钝角,故二面角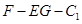 的余弦值为
的余弦值为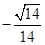 。
。
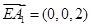 ,则点
,则点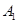 到平面
到平面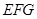 的距离为
的距离为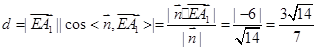 。
。
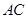 的中点
的中点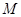 ,连结
,连结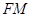 ,则
,则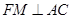 。
。
∵三棱柱
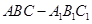 为在直三棱柱,
为在直三棱柱,∴
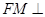 面
面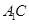 ,∴
,∴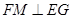 。
。过
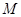 作
作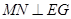 于
于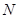 ,连结
,连结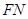 ,则
,则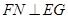 。
。∴
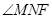 为二面角
为二面角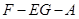 的平面角。
的平面角。在
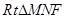 中,
中,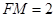 ,
,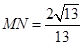 ,则
,则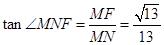 ,得
,得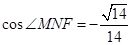 。
。而二面角
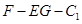 与二面角
与二面角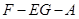 互补,故二面角
互补,故二面角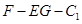 的余弦值为
的余弦值为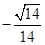 。
。设点
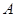 到平面
到平面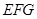 的距离为
的距离为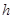 ,由
,由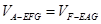 ,得
,得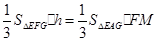 ,即
,即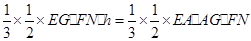 ,∴
,∴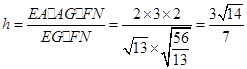 。
。∵点
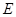 是
是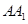 的中点,∴
的中点,∴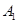 到平面
到平面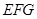 的距离与点
的距离与点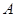 到平面
到平面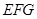 的距离相等,为
的距离相等,为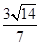 。
。方法二:建立如图所示直角坐标系
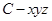 ,则
,则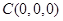 ,
,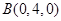 ,
,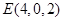 ,
,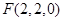 ,
,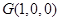 ,
,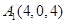 。
。
向量
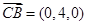 为平面
为平面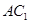 的一个法向量。
的一个法向量。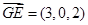 ,
,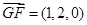 。
。设
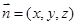 为平面
为平面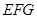 的法向量,则
的法向量,则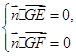 ,即
,即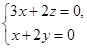 ,取
,取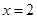 ,得平面
,得平面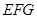 的一个法向量为
的一个法向量为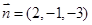 。
。得
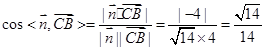 。由图知,二面角
。由图知,二面角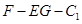 为钝角,故二面角
为钝角,故二面角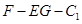 的余弦值为
的余弦值为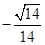 。
。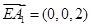 ,则点
,则点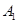 到平面
到平面 的距离为
的距离为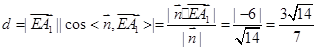 。
。
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 和平面
和平面 ,且
,且 ,则
,则 与
与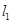 ,
,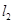 互相平行的一个充分条件是( )
互相平行的一个充分条件是( )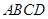 中,
中,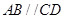 ,
,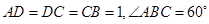 ,四边形
,四边形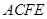 为矩形,平面
为矩形,平面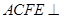 平面
平面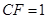 .
.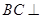 平面
平面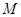 在线段
在线段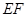 上运动,设平面
上运动,设平面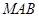 与平面
与平面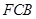 所成二面角的平面角为
所成二面角的平面角为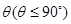 ,试求
,试求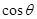 的取值范围.
的取值范围.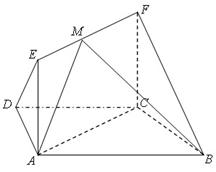
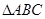 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点,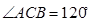 ,
,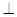 DE?证明你的结论.
DE?证明你的结论.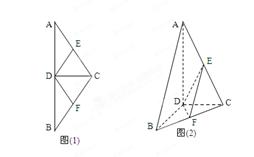
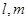 是两条不同的直线,
是两条不同的直线,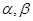 是两个不同的平面,给出下列四个命题:
是两个不同的平面,给出下列四个命题: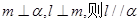 ; ②若
; ②若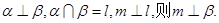
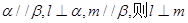 ; ④若
; ④若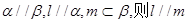 .
.


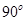

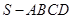 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的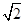 倍,
倍,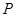 为侧棱
为侧棱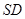 上的点。
上的点。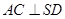 ;
; 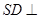 平面
平面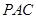 ,求二面角
,求二面角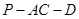 的大小;
的大小;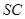 上是否存在一点
上是否存在一点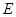 , 使得
, 使得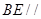 平面
平面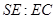 的值;若不存在,试说明理由。
的值;若不存在,试说明理由。