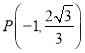题目内容
【题目】已知向量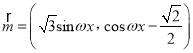
， 
（
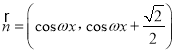），若
，且
的图象上两相邻对称轴间的距离为
.
（Ⅰ）求
的单调递减区间；
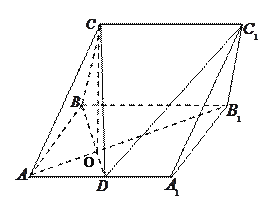
（Ⅱ）设
的内角
， 
， 
的对边分别为
， 
， 
，且满足
， 
， 
，求
， 
的值.
【答案】（Ⅰ）
， 
；（Ⅱ）.
【解析】试题分析： 
利用数量积的坐标运算得到
的解析式，降幂后利用两角和的正弦化简，根据
的图象上两相邻对称轴间的距离为
，求得
值，得到具体的函数解析式，再由相位位于正弦函数的减区间内求得
的 范围得答案。
由
求得
，写出余弦定理，结合
，联立方程组求得
， 
的值。
解析：（Ⅰ）∵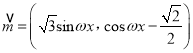
， 
，
∴
.
∵
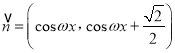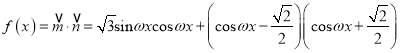
的图像上两相邻对称轴间的距离为
，∴
，即
.
∴
则
.
由
，得
， 
，
∴
的单调减区间为
， 
（Ⅱ）由
，得
，
∵
，∴
，则
， 
.
由余弦定理得： 
，即
，①
又
，②
联立①②解得： 
， 
.
练习册系列答案
相关题目
