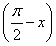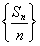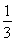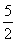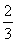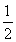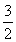题目内容
已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P为椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线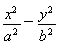 =1写出具有类似特性的性质,并加以证明.
=1写出具有类似特性的性质,并加以证明.
若M、N是双曲线: =1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM,kPN时,那么kPM与kPN之积是与点P位置无关的定值.
=1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM,kPN时,那么kPM与kPN之积是与点P位置无关的定值.
【解析】类似的性质为:若M、N是双曲线: =1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM,kPN时,那么kPM与kPN之积是与点P位置无关的定值.证明如下:
=1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM,kPN时,那么kPM与kPN之积是与点P位置无关的定值.证明如下:
设点M的坐标为(m,n),则点N的坐标为(-m,-n),其中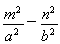 =1.
=1.
又设点P的坐标为(x,y),由kPM=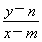 ,kPN=
,kPN= ,得kPM·kPN=
,得kPM·kPN=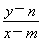 ·
· =
=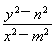 ,
,
将y2=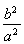 x2-b2,n2=
x2-b2,n2=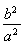 m2-b2代入得kPM·kPN=
m2-b2代入得kPM·kPN=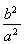 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目