Question

设数列{an}、{bn}、{cn}满足：bn＝an－an＋2，cn＝an＋2an＋1＋3an＋2(n＝1，2，3，…)，求证：{an}为等差数列的充分必要条件是{cn}为等差数列且bn≤bn＋1(n＝1，2，3，…)．

 

Answer 1

见解析

【解析】必要性：

设{an}是公差为d1的等差数列，则

bn＋1－bn＝(an＋1－an＋3)－(an－an＋2)

＝(an＋1－an)－(an＋3－an＋2)＝d1－d1＝0，

所以bn≤bn＋1(n＝1，2，3，…)成立．

又cn＋1－cn＝(an＋1－an)＋2(an＋2－an＋1)＋3(an＋3－an＋2)＝d1＋2d1＋3d1＝6d1(常数)(n＝1，2，3，…)，

所以数列{cn}为等差数列．

充分性：

设数列{cn}是公差为d2的等差数列，且bn≤bn＋1(n＝1，2，3，…)．

∵cn＝an＋2an＋1＋3an＋2，①

∴cn＋2＝an＋2＋2an＋3＋3an＋4，②

①－②，得cn－cn＋2＝(an－an＋2)＋2(an＋1－an＋3)＋3(an＋2－an＋4)＝bn＋2bn＋1＋3bn＋2.

∵cn－cn＋2＝(cn－cn＋1)＋(cn＋1－cn＋2)＝－2d2，

∴bn＋2bn＋1＋3bn＋2＝－2d2，③

从而有bn＋1＋2bn＋2＋3bn＋3＝－2d2，④

④－③，得(bn＋1－bn)＋2(bn＋2－bn＋1)＋3(bn＋3－bn＋2)＝0.⑤

∵bn＋1－bn≥0，bn＋2－bn＋1≥0，bn＋3－bn＋2≥0，

∴由⑤得bn＋1－bn＝0(n＝1，2，3，…)．

由此不妨设bn＝d3(n＝1，2，3，…)，则an－an＋2＝d3(常数)．

由此cn＝an＋2an＋1＋3an＋2?cn＝4an＋2an＋1－3d3，

从而cn＋1＝4an＋1＋2an＋2－5d3，

两式相减得cn＋1－cn＝2(an＋1－an)－2d3，

因此an＋1－an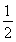＝(cn＋1－cn)＋d3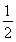＝d2＋d3(常数)(n＝1，2，3，…)，

∴数列{an}为等差数列．