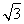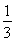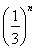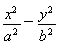题目内容
已知f(n)=1+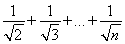 n∈N?),g(n)=2(
n∈N?),g(n)=2(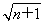 -1)(n∈N?).
-1)(n∈N?).
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
(1)当n=1时,f(1)>g(1);当n=2时,f(2)>g(2);当n=3时,f(3)>g(3).(2)f(n)>g(n)(n∈N*),
【解析】(1)当n=1时,f(1)>g(1);当n=2时,f(2)>g(2);当n=3时,f(3)>g(3).
(2)猜想:f(n)>g(n)(n∈N*),即1+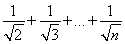 >2(
>2(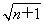 -1)(n∈N*).
-1)(n∈N*).
下面用数学归纳法证明:①当n=1时,f(1)=1,g(1)=2(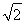 -1),f(1)>g(1).
-1),f(1)>g(1).
②假设当n=k时,猜想成立,即1+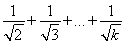 >2(
>2( -1).
-1).
则当n=k+1时,f(k+1)=1+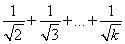 +
+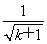 >2(
>2(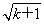 -1)+
-1)+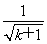 =2
=2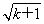 +
+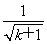 -2,而g(k+1)=2(
-2,而g(k+1)=2(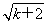 -1)=2
-1)=2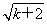 -2,
-2,
下面转化为证明: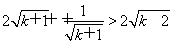 .
.
只要证:2(k+1)+1=2k+3>2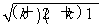 ,
,
需证:(2k+3)2>4(k+2)(k+1),即证:4k2+12k+9>4k2+12k+8,此式显然成立.
所以,当n=k+1时猜想也成立.综上可知:对n∈N*,猜想都成立,
即1+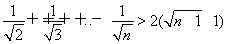 (n∈N*)成立.
(n∈N*)成立.

练习册系列答案
相关题目