题目内容
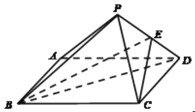
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的动点.记
的动点.记![]() 与
与![]() 所成角的最小值为
所成角的最小值为![]() ,当
,当![]() 为线段
为线段![]() 中点时,二面角
中点时,二面角![]() 的大小为
的大小为![]() ,二面角
,二面角![]() 的大小为
的大小为![]() ,则
,则![]() ,
,![]() ,
,![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
BE与AP所成角的最小值即为AP与平面PBD所成的角,利用空间中的线与线、线与平面的垂直关系可得![]() 与平面PBD所成的角即为
与平面PBD所成的角即为![]() ,设
,设![]() 即表示
即表示![]() ;利用一线定角表示
;利用一线定角表示![]() 与
与![]() ,分别计算其正切值,即可比较大小.
,分别计算其正切值,即可比较大小.
BE与AP所成角的最小值即为AP与平面PBD所成的角.
![]() 平面PCD,
平面PCD,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() 面PAD,
面PAD,
![]() ,又
,又![]() ,
,![]() 面PAB,
面PAB,
而![]() 面PBD,
面PBD,![]() 面
面![]() 面PAB,
面PAB,
![]() 与平面PBD所成的角即为
与平面PBD所成的角即为![]() ,
,
即![]() .
.
不妨设![]() ,则
,则![]() ,
,![]() .
.
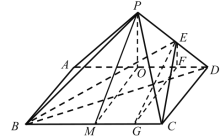
在平面PAD内作![]() ,
,![]() 面
面![]() 面ABCD,
面ABCD,![]() 面ABCD,
面ABCD,
在面ABCD内作![]() ,连PM,则
,连PM,则![]() ,
,
![]() 即为二面角
即为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ﹒
﹒
同理,作![]() ,
,![]() ,连
,连![]() ,则
,则![]() ,
,
![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]() .
.
易知: ﹒
﹒![]() ,
,
![]() ,
,![]() ﹒
﹒
故选:B

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目