题目内容
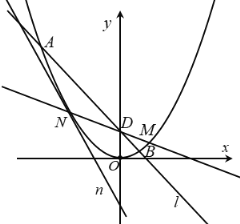
【题目】如图,在平面直角坐标系xOy中,点![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() 与抛物线C交于A,B两点,且直线OA,OB的斜率之和为
与抛物线C交于A,B两点,且直线OA,OB的斜率之和为![]() .
.
(1)求a和k的值;
(2)若![]() ,设直线
,设直线![]() 与y轴交于D点,延长MD与抛物线C交于点N,抛物线C在点N处的切线为n,记直线n,
与y轴交于D点,延长MD与抛物线C交于点N,抛物线C在点N处的切线为n,记直线n,![]() 与x轴围成的三角形面积为S.求S的最小值.
与x轴围成的三角形面积为S.求S的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)将点![]() 代入抛物线
代入抛物线![]() ,得
,得![]() ,设
,设![]() ,
,![]() ,
,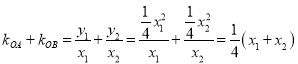 ,将直线
,将直线![]() 的方程与抛物线方程联立,可得出
的方程与抛物线方程联立,可得出![]() 的值.
的值.
(2)由(1)得直线![]() 的方程
的方程![]() ,可得
,可得![]() ,所以
,所以![]() ,则直线DM的方程为:
,则直线DM的方程为:![]() ,联立
,联立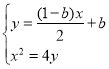 ,可得到
,可得到![]() ,利用导数求出切线n的方程,解出点
,利用导数求出切线n的方程,解出点![]() 的坐标,得到三角形的面积表达式,利用导数求出最大值.
的坐标,得到三角形的面积表达式,利用导数求出最大值.
解:(1)将点![]() 代入抛物线
代入抛物线![]() ,得
,得![]() ,
,
由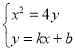 ,得
,得![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
故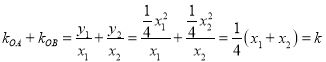
由已知直线OA.OB的斜率之和为![]() ,故
,故![]() ;
;
(2)在直线![]() 的方程
的方程![]() 中,
中,
令![]() 得
得![]() ,
,![]() ,
,
直线DM的方程为:![]() ,
,
即![]()
由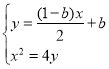 ,得
,得![]() ,
,
解得:![]() 或
或![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,
,
切线n的斜率![]() ,
,
切线n的方程为:![]() ,即
,即![]() ,
,
由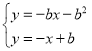 ,得直线l、n交点Q,纵坐标
,得直线l、n交点Q,纵坐标![]()
设直线![]() ,
,![]() 与x轴的交点
与x轴的交点![]() ,
,![]() ,
,
在直线![]() ,
,![]() 方程中令
方程中令![]() .
.
得到点![]() ,
,![]() ,
,
所以![]() ,
,
![]() ,
,![]() .
.
当![]() ,函数单调递减;当
,函数单调递减;当![]() 时,函数单调递增;
时,函数单调递增;
∴当![]() 时,S最小值为
时,S最小值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加,下表是某购物网站![]() 年
年![]() 月促销费用
月促销费用![]() (万元)和产品销量
(万元)和产品销量![]() (万件)的具体数据.
(万件)的具体数据.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促销费用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() (系数精确到
(系数精确到![]() );
);
(2)已知![]() 月份该购物网站为庆祝成立
月份该购物网站为庆祝成立![]() 周年,特定制奖励制度:用
周年,特定制奖励制度:用![]() (单位:件)表示日销量,若
(单位:件)表示日销量,若![]() ,则每位员工每日奖励
,则每位员工每日奖励![]() 元;若
元;若![]() ,每位员工每日奖励
,每位员工每日奖励![]() 元;若
元;若![]() ,则每位员工每日奖励
,则每位员工每日奖励![]() 元.现已知该网站
元.现已知该网站![]() 月份日销量
月份日销量![]() 服从正态分布
服从正态分布![]() ,请你计算某位员工当月奖励金额总数大约为多少元.(当月奖励金额总数精确到百分位)
,请你计算某位员工当月奖励金额总数大约为多少元.(当月奖励金额总数精确到百分位)
参考数据:![]() ,
,![]() ,其中
,其中![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量,![]() .
.
参考公式:①对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
②若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .
.
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求![]() 的值;
的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |