Question

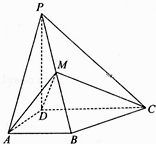
【题目】在棱长为6的正方体ABCD﹣A1B1C1D1中，M是BC的中点，点P是面DCC1D1内的动点，且满足∠APD=∠MPC，则三棱锥P﹣BCD的体积最大值是（ ）
A.36
B.12
C.24
D.18

Answer 1

【答案】B
【解析】解：∵在棱长为6的正方体ABCD﹣A1B1C1D1中，M是BC的中点，点P是面DCC1D1所在的平面内的动点，且满足∠APD=∠MPC， ∴Rt△ADP∽△Rt△PMC，
∴ = =2，
即PD=2PC，
设DO=x，PO=h，作PO⊥CD，
∴ ，化简得：3h2=﹣3x2+48x﹣144，0≤x≤6，
根据函数单调性判断：x=6时，3h2最大值为36，
h大=2 ，
∵在正方体中PO⊥面BCD，
∴三棱锥P﹣BCD的体积最大值： =12 ，
故选：B