题目内容
设f（x）是定义在R上的偶函数，它在[0，+∞）上为增函数，且f（
）＞0，则不等式f（
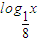）＞0的解集为（ ）A．（0，
）B．（2，+∞）
C．（
，1）∪（2，+∞）D．（0，
）∪（2，+∞）
【答案】分析：根据题意，由f（
）＞0可得
，从而可得不等式f（
）＞0的解集．
解答：解：∵f（x）是定义在R上的偶函数，∴f（-x）=f（x）=f（|x|），
又f（x）在[0，+∞）上为增函数，且f（
）＞0，
∴由f（
）＞0，可得
，即
，
∴
；
故选D．
点评：本题考查函数奇偶性与单调性的综合，难点在于对偶函数f（x）=f（|x|）的深刻理解与应用，属于中档题．
）＞0可得，从而可得不等式f（）＞0的解集．解答：解：∵f（x）是定义在R上的偶函数，∴f（-x）=f（x）=f（|x|），
又f（x）在[0，+∞）上为增函数，且f（
）＞0，∴由f（
）＞0，可得，即
，∴
；故选D．
点评：本题考查函数奇偶性与单调性的综合，难点在于对偶函数f（x）=f（|x|）的深刻理解与应用，属于中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
设f（x）是定义在R上的奇函数，且对任意实数x，恒有f（x+2）=-f（x）．当x∈[0，2]时，f（x）=2x-x2+a（a是常数）．则x∈[2，4]时的解析式为（ ）
| A、f（x）=-x2+6x-8 | B、f（x）=x2-10x+24 | C、f（x）=x2-6x+8 | D、f（x）=x2-6x+8+a |