Question

【题目】在平面直角坐标系中，设点，定义，其中为坐标原点，对于下列结论：

符合的点的轨迹围成的图形面积为8；

设点是直线：上任意一点，则；

设点是直线：上任意一点，则使得“最小的点有无数个”的充要条件是；

设点是椭圆上任意一点，则．

其中正确的结论序号为　　

A. B. C. D.

Answer 1

【答案】D

【解析】

根据新定义由，讨论、的取值，画出分段函数的图象，求出面积即可；运用绝对值的含义和一次函数的单调性，可得的最小值；根据等于1或都能推出最小的点有无数个可判断其错误；把的坐标用参数表示，然后利用辅助角公式求得的最大值说明命题正确．

由，根据新定义得：，由方程表示的图形关于轴对称和原点对称，且，画出图象如图所示：

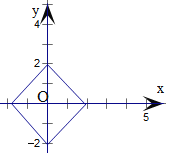
四边形为边长是的正方形，面积等于8，故正确；

为直线上任一点，可得，

可得，

当时，；当时，；

当时，可得，综上可得的最小值为1，故正确；

，当时，，满足题意；

而，当时，，满足题意，即都能 “使最小的点有无数个”，不正确；

点是椭圆上任意一点，因为求最大值，所以可设，，，，，，正确．

则正确的结论有：、、，故选D．