题目内容
【题目】下列命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
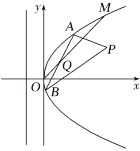
②在直角坐标系![]() 中,点
中,点![]() ,将向量
,将向量![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到向量
得到向量![]() ,则点
,则点![]() 的坐标是
的坐标是![]() ;
;
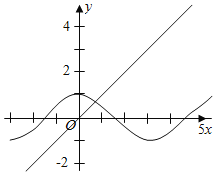
③在同一直角坐标系中,函数![]() 的图象和函数
的图象和函数![]() 的图象有两个公共点;
的图象有两个公共点;
④函数![]() 在
在![]() 上是增函数.
上是增函数.
其中,正确的命题是________(填正确命题的序号).
【答案】①②④
【解析】
由余弦函数的周期公式可判断①;由任意角的三角函数定义可判断②;由余弦函数和一次函数的图象可判断③;由诱导公式和余弦函数的单调性可判断④.
函数y=cos(﹣2x)即y=cos2x的最小正周期是π,故①正确;
在直角坐标系xOy中,点P(a,b),
将向量![]() 绕点O逆时针旋转90°得到向量
绕点O逆时针旋转90°得到向量![]() ,
,
设a=rcosα,b=rsinα,可得rcos(90°+α)=﹣rsinα=﹣b,
rsin(90°+α)=rcosα=a,则点Q的坐标是(﹣b,a),故②正确;
在同一直角坐标系中,函数y=cosx的图象和函数y=x的图象有一个公共点,故③错误;
函数y=sin(x![]() )即y=﹣cosx在[0,π]上是增函数,故④正确.
)即y=﹣cosx在[0,π]上是增函数,故④正确.
故答案为:①②④.

练习册系列答案
相关题目