题目内容
【题目】在直角坐标系xOy中,直线l1的参数方程为 ![]() ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为  ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(Ⅰ)写出C的普通方程;
(Ⅱ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣ ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
【答案】解:(Ⅰ)∵直线l1的参数方程为 ![]() ,(t为参数),
,(t为参数),
∴消掉参数t得:直线l1的普通方程为:y=k(x﹣2)①;
又直线l2的参数方程为 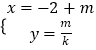 ,(m为参数),
,(m为参数),
同理可得,直线l2的普通方程为:x=﹣2+ky②;
联立①②,消去k得:x2﹣y2=4,即C的普通方程为x2﹣y2=4;
(Ⅱ)∵l3的极坐标方程为ρ(cosθ+sinθ)﹣ ![]() =0,
=0,
∴其普通方程为:x+y﹣ ![]() =0,
=0,
联立 ![]() 得:
得: 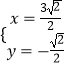 ,
,
∴ρ2=x2+y2= ![]() +
+ ![]() =5.
=5.
∴l3与C的交点M的极径为ρ= ![]() .
.
【解析】解:(Ⅰ)分别消掉参数t与m可得直线l1与直线l2的普通方程为y=k(x﹣2)①与x=﹣2+ky②;联立①②,消去k可得C的普通方程为x2﹣y2=4;
(Ⅱ)将l3的极坐标方程为ρ(cosθ+sinθ)﹣ ![]() =0化为普通方程:x+y﹣
=0化为普通方程:x+y﹣ ![]() =0,再与曲线C的方程联立,可得
=0,再与曲线C的方程联立,可得 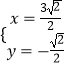 ,即可求得l3与C的交点M的极径为ρ=
,即可求得l3与C的交点M的极径为ρ= ![]() .
.
【考点精析】利用极坐标系和直线的参数方程对题目进行判断即可得到答案,需要熟知平面内取一个定点O,叫做极点;自极点O引一条射线OX叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系;经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为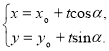 (
(![]() 为参数).
为参数).

练习册系列答案
相关题目


