题目内容
【题目】已知奇函数![]() 与偶函数
与偶函数![]() 均为定义在
均为定义在![]() 上的函数,并满足
上的函数,并满足![]()
(1)求![]() 的解析式;
的解析式;
(2)设函数![]()
①判断![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
②若![]() ,求实数
,求实数![]() 的取值范围
的取值范围
【答案】(1) ![]() (2)
(2) ![]() 为
为![]() 上的单增函数;证明见解析;① ②
上的单增函数;证明见解析;① ②![]()
【解析】
(1)利用解方程法,把![]() 看成两个未知数,构造两个方程,从而求得
看成两个未知数,构造两个方程,从而求得![]() 的表达式;
的表达式;
(2)①易得![]() 为
为![]() 上的单增函数,再利用定义单调性的三个步骤,即一取、二比、三下的完整步骤进行证明;
上的单增函数,再利用定义单调性的三个步骤,即一取、二比、三下的完整步骤进行证明;
②利用换元法,令![]() 将不等式转化为
将不等式转化为![]() ,再利用单调性得到
,再利用单调性得到![]() ,最后求得实数
,最后求得实数![]() 的取值范围.
的取值范围.
(1)因为奇函数![]() 与偶函数
与偶函数![]() 均为定义在
均为定义在![]() 上的函数,
上的函数,
所以![]() ,
,![]()
因为![]() ,①
,①
所以![]() ,
,
即![]() ②
②
①-②得:![]() ,所以
,所以![]() ;
;
(2)①![]() 为
为![]() 上的单增函数,以下给出证明:
上的单增函数,以下给出证明:
因为![]() ,设
,设![]() ,则:
,则:
![]()
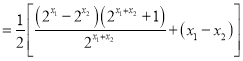
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以![]() 为
为![]() 上的单增函数;
上的单增函数;
②设![]() ,则
,则![]() ,即
,即![]()
即![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() 为奇函数,
为奇函数,
由![]() ,得
,得![]() ,又
,又![]() 为
为![]() 上的增函数,
上的增函数,
所以![]() 等价于
等价于![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】下面四个命题,
(1)函数![]() 在第一象限是增函数;
在第一象限是增函数;
(2)在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充分非必要条件;
”的充分非必要条件;
(3)函数![]() 图像关于点
图像关于点![]() 对称的充要条件是
对称的充要条件是![]() ;
;
(4)若![]() ,则
,则![]() .
.
其中真命题的是_________.(填所有真命题的序号)
【题目】某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分两层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2:
表1:
生产能力分组 |
|
|
|
|
|
人数 | 4 | 8 | x | 5 | 3 |
表2:
生产能力分组 |
|
|
|
|
人数 | 6 | y | 36 | 18 |
(1)求x,y的值;
(2)在答题纸上完成频率分布直方图;并根据频率分布直方图,估计该工厂B类工人生产能力的平均数(同一组中的数据用该区间的中点值作代表)和中位数.(结果均保留一位小数)


【题目】某大型商场去年国庆期间累计生成![]() 万张购物单,从中随机抽出
万张购物单,从中随机抽出![]() 张,对每单消费金额进行统计得到下表:
张,对每单消费金额进行统计得到下表:
消费金额(单位:元) |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 | 10 | 10 |
由于工作人员失误,后两栏数据已无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率,完成下列问题:
(1)估计去年国庆期间该商场累计生成的购物单中,单笔消费额超过![]() 元的概率;
元的概率;
(2)为鼓励顾客消费,该商场打算在今年国庆期间进行促销活动,凡单笔消费超过![]() 元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值
元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值![]() 元、
元、![]() 元、
元、![]() 元的奖品.已知中奖率为
元的奖品.已知中奖率为![]() ,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为
,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为![]() .若今年国庆期间该商场的购物单数量比去年同期增长
.若今年国庆期间该商场的购物单数量比去年同期增长![]() ,式预测商场今年国庆期间采办奖品的开销.
,式预测商场今年国庆期间采办奖品的开销.



