题目内容
设曲线y=(ax﹣1)ex在点A(x0,y1)处的切线为l1,曲线y=(1﹣x)e﹣x在点B(x0,y2)处的切线为l2.若存在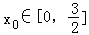 ,使得l1⊥l2,则实数a的取值范围为 .
,使得l1⊥l2,则实数a的取值范围为 .
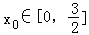 ,使得l1⊥l2,则实数a的取值范围为 .
,使得l1⊥l2,则实数a的取值范围为 .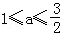
试题分析:根据曲线方程分别求出导函数,把A和B的横坐标x0分别代入到相应的导函数中求出切线l1和切线为l2的斜率,然后根据两条切线互相垂直得到斜率乘积为﹣1,列出关于等式由
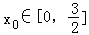 解出
解出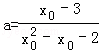 ,然后根据
,然后根据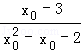 为减函数求出其值域即可得到a的取值范围.
为减函数求出其值域即可得到a的取值范围.函数y=(ax﹣1)ex的导数为y′=(ax+a﹣1)ex,
∴l1的斜率为
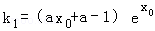 ,
,函数y=(1﹣x)e﹣x的导数为y′=(x﹣2)e﹣x
∴l2的斜率为
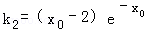 ,
,由题设有k1•k2=﹣1从而有
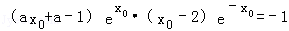
∴a(x02﹣x0﹣2)=x0﹣3
∵
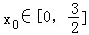 得到x02﹣x0﹣2≠0,所以
得到x02﹣x0﹣2≠0,所以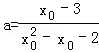 ,
,又a′=
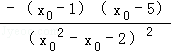 ,另导数大于0得1<x0<5,
,另导数大于0得1<x0<5,故
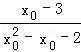 在(0,1)是减函数,在(1,
在(0,1)是减函数,在(1,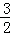 )上是增函数,
)上是增函数,x0=0时取得最大值为
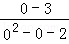 =
=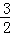 ;
;x0=1时取得最小值为1.
∴
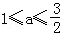
点评:此题是一道综合题,考查学生会利用导数求切线的斜率,会求函数的值域,掌握两直线垂直时斜率的关系

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
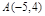 和
和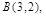 求过点
求过点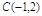 且与
且与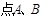 的距离相等的直线方程.
的距离相等的直线方程.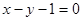 的倾斜角是( )
的倾斜角是( )

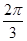

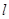 过点P(-2,1),
过点P(-2,1),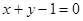 平行,求直线
平行,求直线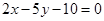 与坐标轴所围成的三角形的面积为
与坐标轴所围成的三角形的面积为 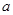 ,1+
,1+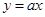 与
与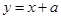 正确的是( )
正确的是( )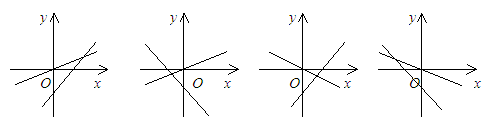
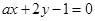 与直线
与直线 垂直,那么实数
垂直,那么实数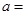 .
.