题目内容
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且acosC=(2b﹣c)cosA.
(1)若![]() 3,求△ABC的面积;
3,求△ABC的面积;
(2)若∠B<∠C,求2cos2B+cos2C的取值范围.
【答案】(1)![]() (2)(
(2)(![]() ,
,![]() ).
).
【解析】
(1)利用正弦定理可求角A,结合数量积![]() 3,可求△ABC的面积;
3,可求△ABC的面积;
(2)结合角之间的关系,把2cos2B+cos2C化简为![]() ,然后结合角
,然后结合角![]() 的范围可求.
的范围可求.
(1)∵acosC=(2b﹣c)cosA,
∴由正弦定理可得sinAcosC=(2sinB﹣sinC)cosA,可得sinAcosC+sinCcosA=sin(A+C)=sinB=2sinBcosA,
∵B为三角形内角,sinB≠0,
∴cosA![]() ,
,
又∵A∈(0,π),
∴A![]() ,
,
∵![]() bccosA
bccosA![]() bc=3,可得bc=6,
bc=3,可得bc=6,
∴S△ABC![]() bcsinA
bcsinA![]() .
.
(2)∵∠B<∠C,C![]() B,可得B∈(0,
B,可得B∈(0,![]() ),
),
∴2B![]() ∈(
∈(![]() ,
,![]() ),
),
∴cos(2B![]() )∈(
)∈(![]() ,
,![]() ),
),
∴2cos2B+cos2C=1+cos2B![]() cos2B
cos2B![]() cos2(
cos2(![]() B)
B)![]() cos2B
cos2B![]() cos2B
cos2B![]() sin2B
sin2B![]() cos(2B
cos(2B![]() )∈(
)∈(![]() ,
,![]() ).
).
∴2cos2B+cos2C的取值范围(![]() ,
,![]() ).
).

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式: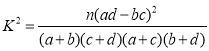 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |