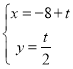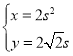Question

【题目】已知圆O：x2+y2＝3上的一动点M在x轴上的投影为N，点P满足．

（1）求动点P的轨迹C的方程；

（2）若直线l与圆O相切，且交曲线C于点A，B，试求|AB|的最大值．

Answer 1

【答案】（1）3x2+2y2＝9．（2）最大值为2

【解析】

（1）设根据已知，将点坐标用表示，代入圆方程，即可求解；

（2）设直线l的方程为，根据条件求出关系，将直线方程与椭圆方程联立，消去，得到关于的方程，利用根与系数关系，求出关于的函数，利用换元法，运用函数的单调性，即可求解.

（1）设P（x，y），M（x0，y0），则N（x0，0），∵，

∴（x 0﹣x，0﹣y）（0，0﹣y0），即有，

点M在圆O：x2+y2＝3上所以x02+y02＝3，

代入得，

∴点P的轨迹C为．

（2）由已知可得当直线l的斜率不存在时不合题意．

故可设直线l的方程为y＝kx+t，即kx﹣y+t＝0．

∵圆O与直线l相切，∴圆O到直线l的距离，

∴t2＝3（k2+1），

由可得（3+2k2）x2+4ktx+2t2﹣9＝0，

恒成立．

设A（x1，y1），B（x2，y2），则，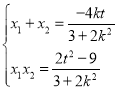

∵t2＝3（k2+1），

∴|AB|

，

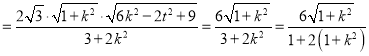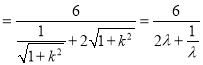，其中．

令，λ∈[1，+∞）．

∵恒成立，∴g（λ）在[1，+∞）上单调递增，

∴g（λ）≥g（1）＝3，即，，

．

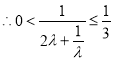故|AB|的最大值为2，当且仅当λ＝1，即k＝0时取等号．