题目内容
【题目】如图,椭圆的中心为原点O,长轴在x轴上,离心率![]() ,过左焦点F1作x轴的垂线交椭圆于A,
,过左焦点F1作x轴的垂线交椭圆于A,![]() 两点
两点![]() .
.
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P,![]() ,过P、
,过P、![]() 作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若
作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若![]() ,求圆Q的标准方程.
,求圆Q的标准方程.

【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(1)先将点坐标代入椭圆方程,再与离心率联立方程组解得a,b,(2)根据题意得点P![]() 是椭圆上到点
是椭圆上到点![]() 的距离最小的点,因此先建立椭圆上任意一点到Q距离的函数关系式,根据二次函数性质确定最小值取法得
的距离最小的点,因此先建立椭圆上任意一点到Q距离的函数关系式,根据二次函数性质确定最小值取法得![]() ,再根据
,再根据![]() 得P点纵坐标,最后根据P点在椭圆上解得
得P点纵坐标,最后根据P点在椭圆上解得![]() ,即得圆Q的标准方程.
,即得圆Q的标准方程.
试题解析:(Ⅰ)由题意知,![]() 在椭圆上,
在椭圆上,
则![]() ,从而
,从而![]()
由![]() ,得
,得![]() ,从而
,从而![]() .
.
故该椭圆的标准方程为![]()
(Ⅱ)由椭圆的对称性,可设![]() .
.
又设![]() 是椭圆上任意一点,则
是椭圆上任意一点,则
![]()
![]()
设![]() ,由题意知,点P是椭圆上到点Q的距离最小的点,
,由题意知,点P是椭圆上到点Q的距离最小的点,
因此,上式当![]() 时取最小值.
时取最小值.
又因为![]() ,∴上式当
,∴上式当![]() 时取最小值,
时取最小值,
从而![]() ,且
,且![]() .因为
.因为![]() ,且
,且![]() ,
,
∴![]() ,即
,即![]()
由椭圆方程及![]() ,得
,得![]() ,
,
解得![]() ,从而
,从而![]() .
.
故这样的圆有两个,其标准方程分别为
![]()

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
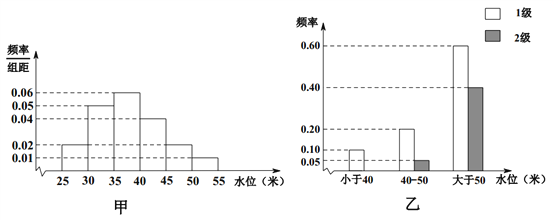
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.




