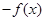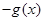题目内容
已知函数y=f(x)的图象如图所示,则不等式f(x)-f(-x)>-1的解集是______.
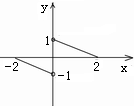

由图象可得函数的解析式为f(x)=
∴由f(x)-f(-x)>-1得
当0≤x≤2时,f(x)-f(-x)>-1?-
x+1-(
x-1)>-1?x<3,此时 0≤x≤2;
当-2≤x<0时,f(x)-f(-x)>-1?-
x-1-(
x+1)?x<-1,此时-2≤x<-1.
综上所述,不等式f(x)-f(-x)>-1的解集是[0,2]∪[-2,-1).
故答案为[0,2]∪[-2,-1).
|
∴由f(x)-f(-x)>-1得
当0≤x≤2时,f(x)-f(-x)>-1?-
| 1 |
| 2 |
| 1 |
| 2 |
当-2≤x<0时,f(x)-f(-x)>-1?-
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,不等式f(x)-f(-x)>-1的解集是[0,2]∪[-2,-1).
故答案为[0,2]∪[-2,-1).

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
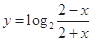 的图像( ).
的图像( ).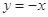 对称
对称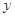 轴对称
轴对称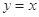 对称
对称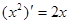 ,
,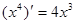 ,
,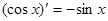 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在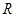 上的函数
上的函数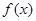 满足
满足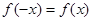 ,记
,记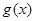 为
为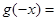 ( )
( )