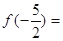题目内容
若函数f(x)=
是R上的单调函数,则实数a取值范围为( )
|
| A.(1,+∞) | B.(1,8) | C.(4,8) | D.[4,8) |
①若函数f(x)单调性递增,
则满足
,即
,解得4≤a<8.
②若函数f(x)单调性递减,
则满足
,即
,此时无解.
综上实数a取值范围为:4≤a<8.
故选D.
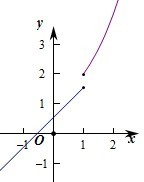
则满足
|
|
②若函数f(x)单调性递减,
则满足
|
|
综上实数a取值范围为:4≤a<8.
故选D.


练习册系列答案
相关题目
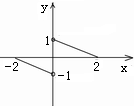
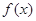 是周期为
是周期为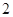 的偶函数,当
的偶函数,当 时,
时, 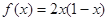 ,则
,则