题目内容
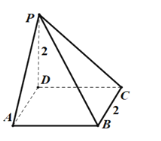
【题目】设椭圆
的左、右焦点分别为
，
、
，，点
在椭圆上，
为原点.
⑴若
，
，求椭圆的离心率；
⑵若椭圆的右顶点为
，短轴长为2，且满足
为椭圆的离心率）.
①求椭圆的方程；
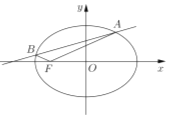
②设直线
：
与椭圆相交于、
两点，若
的面积为1，求实数
的值.
【答案】（1）
（2）①
②
【解析】
（1）由题意得
，利用勾股定理得
，再利用椭圆的定义得到
的关系，从而求得离心率；
（2）①由
，得
，求出
后，即可得到椭圆的方程；
②设点
，将直线方程代入椭圆方程，利用韦达定理和弦长公式求得
关于
的解析式，再由点到直线的距离公式，得到面积
，从而求得的值.
（1）连接
.因为
，
所以
是等边三角形，所以
.
又
，所以,所以.
于是，有
，
所以
，即所求椭圆的离心率为.
（2）①由，得
，
整理，得.
又因为
，所以
，
.
故所求椭圆的方程为.
②依题意，设点.
联立方程组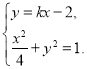
消去
，并整理得
.
则
，（*）
且
，
所以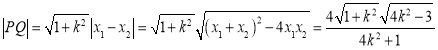
.
又点
到直线
的距离为
，
所以
.
因为
，所以
，解得.
经验证满足（*）式，
故所求实数.
【题目】“互联网+”是“智慧城市”的重要内容，A市在智慧城市的建设中，为方便市民使用互联网，在主城区覆盖了免费WiFi为了解免费WiFi在A市的使用情况，调查机构借助网络进行了问卷调查，并从参与调查的网友中抽取了200人进行抽样分析，得到如下列联表（单位：人）：
经常使用免费WiFi | 尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
（1）根据以上数据，判断是否有90%的把握认为A市使用免费WiFi的情况与年龄有关；
（2）现从所抽取的45岁以上的市民中按是否经常使用WiFi进行分层抽样再抽取5人.
（i）分别求这5人中经常使用，偶尔或不用免费WFi的人数；
（ii）从这5人中，再随机选出2人各赠送1件礼品，求选出的2人中至少有1人经常使用免费WiFi的概率.
附：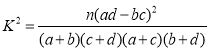
，其中
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
