题目内容
【题目】定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,且
,且![]() .当
.当![]() 时,
时, ![]() .
.
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)当![]() 取何值时,方程
取何值时,方程![]() 在
在![]() 上有解.
上有解.
【答案】(1) ;(2)见解析;(3)
;(2)见解析;(3)![]() ,或
,或![]() ,或
,或![]() .
.
【解析】试题分析:(1)设![]() ,则
,则![]() 结合f(-x)=-f(x),及x∈(0,1)时,
结合f(-x)=-f(x),及x∈(0,1)时, ![]() ,,可求x∈(-1,0)时得f(x),在f(-x)=-f(x)中可求f(0)=0
,,可求x∈(-1,0)时得f(x),在f(-x)=-f(x)中可求f(0)=0
(2)利用函数的单调性的定义证明即可.
(3)方程![]() 在
在![]() 上有解的充要条件是,
上有解的充要条件是, ![]() 在函数
在函数![]() ,
, ![]() 的值域内取值,只需求出函数的值域,然后求解k的范围.
的值域内取值,只需求出函数的值域,然后求解k的范围.
试题解析:
(1)设![]() ,则
,则![]() .
.
∵![]() ,且
,且![]() 时,
时, ![]() ,
,
∴![]() 时,有
时,有![]() .
.
在![]() 中,令
中,令![]() 得
得
![]() .
.
∵![]() ,
, ![]() ,令
,令![]() ,
,
得![]() ,
,
∴![]() ,从而
,从而![]() ,
,
∴当![]() 时,有
时,有
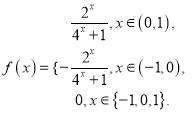 .
.
(2)设![]() ,则
,则![]() ,
,
![]()
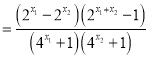 .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
, ![]() .
.
又∵![]() ,
,
∴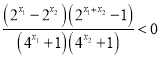 ,
,
即![]() ,∴
,∴![]() 在
在![]() 上是减函数.
上是减函数.
(3)方程![]() 在
在![]() 上有解的充要条件是,
上有解的充要条件是, ![]() 在函数
在函数![]() ,
, ![]() 的值域内取值.
的值域内取值.
∵![]() 时,
时, ![]() 是减函数,
是减函数,
∴![]() 时,
时, ![]() ,
,
即![]() .
.
∵![]() ,∴
,∴![]() 时,
时,
![]() .
.
又![]() ,
,
∴![]() 时,函数
时,函数![]() 的值域为
的值域为![]() .
.
∴当![]() ,或
,或![]() ,或
,或![]() 时,方程
时,方程![]() 在
在![]() 上有解.
上有解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】为调查大学生这个微信用户群体中每人拥有微信群的数量,现从武汉市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量 | 频数 | 频率 |
0至5个 | 0 | 0 |
6至10个 | 30 | 0.3 |
11至15个 | 30 | 0.3 |
16至20个 | a | c |
20个以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值;
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.

