题目内容
1. 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若(1)中过点A作圆C的切线,切点分别为E,F,求弦|EF|的长度.
分析 (1)由$\left\{\begin{array}{l}y=2x-4\\ y=x-1\end{array}\right.$得圆心C,可得圆C的方程,设出切线方程,运用相切的条件d=r,解方程可得k,进而得到切线方程;
(2)由切线方程和圆的方程联立,可得切点的坐标,再由两点的距离公式计算即可得到弦长.
解答 解:(1)由$\left\{\begin{array}{l}y=2x-4\\ y=x-1\end{array}\right.$得圆心C为(3,2),
∵圆C的半径为1,
∴圆C的方程为:(x-3)2+(y-2)2=1,
显然切线的斜率一定存在,
设所求圆C的切线方程为y=kx+3,
∴$\frac{|3k-2+3|}{\sqrt{{k}^{2}+1}}$=1,
∴|3k+1|=$\sqrt{{k}^{2}+1}$,
∴k=0或k=-$\frac{3}{4}$,
∴圆C的切线方程为:y=3或者y=-$\frac{3}{4}$x+3,
即y=3或3x+4y-12=0;
(2)由(1)知$\left\{{\begin{array}{l}{y=3}\\{{{(x-3)}^2}+{{(y-2)}^2}=1}\end{array}}\right.∴\left\{{\begin{array}{l}{x=3}\\{y=1}\end{array}}\right.∴E(3,3)$;
∵$直线FC⊥AF∴{k_{FC}}=\frac{4}{3}∴FC:y=\frac{4}{3}x-2$,
∵$\left\{\begin{array}{l}{3x+4y-12=0}\\{y=\frac{4}{3}x-2}\end{array}\right.$,∴$\left\{\begin{array}{l}{x=\frac{12}{5}}\\{y=\frac{6}{5}}\end{array}\right.$,即F($\frac{12}{5}$,$\frac{6}{5}$).
∴|EF|=$\sqrt{(\frac{12}{5}-3)^{2}+(\frac{6}{5}-3)^{2}}$=$\frac{\sqrt{10}}{5}$.
点评 本题考查直线和圆相切的条件,考查切线方程和切点弦长的求法,考查运算能力,属于中档题.

| A. | (x-2)2+(y-1)2=$\sqrt{5}$ | B. | (x-2)2+(y-1)2=5 | C. | (x+2)2+(y+1)2=$\sqrt{5}$ | D. | (x+2)2+(y+1)2=5 |
| A. | $\frac{8}{3}$ | B. | 8 | C. | 12 | D. | 24 |
| A. | 0或-7 | B. | -7 | C. | 0 | D. | 7 |
 为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.20 |
| [80,90) | 16 | 0.32 |
| [90,100] | ||
| 合计 |
(2)不具体计算频率/组距,补全频率分布直方图.
| A. | 2bn+1=bn+bn+2 | B. | bn+12=bn•bn+2 | C. | 2bn+1=bn•bn+2 | D. | bn+12=bn+bn+2 |
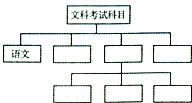 安徽省2015年高考文科考试科目有语文、数学、英语和文综,文综是指政治、历史、地理等三科合在一张卷子上,请你将图补充完整.
安徽省2015年高考文科考试科目有语文、数学、英语和文综,文综是指政治、历史、地理等三科合在一张卷子上,请你将图补充完整.