题目内容
已知椭圆 的右焦点为
的右焦点为 ,点
,点 在圆
在圆 上任意一点(点
上任意一点(点 第一象限内),过点
第一象限内),过点 作圆
作圆 的切线交椭圆
的切线交椭圆 于两点
于两点 、
、 .
.
(1)证明: ;
;
(2)若椭圆离心率为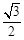 ,求线段
,求线段 长度的最大值.
长度的最大值.
 的右焦点为
的右焦点为 ,点
,点 在圆
在圆 上任意一点(点
上任意一点(点 第一象限内),过点
第一象限内),过点 作圆
作圆 的切线交椭圆
的切线交椭圆 于两点
于两点 、
、 .
.(1)证明:
 ;
;(2)若椭圆离心率为
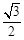 ,求线段
,求线段 长度的最大值.
长度的最大值.
(1)略(2)2
(1) 设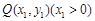 ,先利用焦半径公式表示
,先利用焦半径公式表示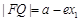 ,然后再想法求出|PQ|,也用x1表示出来.相加即可.
,然后再想法求出|PQ|,也用x1表示出来.相加即可.
(2)根据离心率可求出a值,进而椭圆方程确定,然后设直线 的方程为
的方程为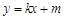 ,由直线QR与圆O相切,进而得到
,由直线QR与圆O相切,进而得到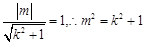 ,
,
然后直线与椭圆方程联立,消y之后,表示出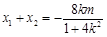 ,
,
则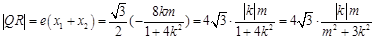 ,
,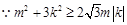 ,
,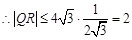 ,因而确定当且仅当
,因而确定当且仅当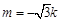 时,
时,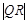 取最大值2.
取最大值2.
(1)设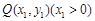 ,得
,得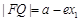 ,…………………3分
,…………………3分
由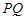 是圆
是圆 的切线,
的切线,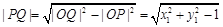 ,
,
注意到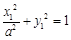 ,
,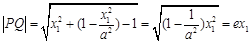 ,……………6分
,……………6分
所以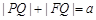 . ……………7分
. ……………7分
(2)由题意,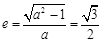 ,
,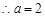 . …………………………9分
. …………………………9分
方法一:设直线 的方程为
的方程为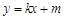 ,
,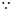 点
点 在第一象限,
在第一象限,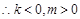 .
.
由直线 与圆
与圆 相切,
相切,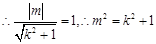 . …………………………11分
. …………………………11分
由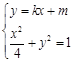 ,消
,消 得
得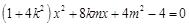 ,
,
设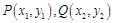 ,则
,则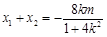 .
.
由(1)知,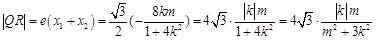 ,…14分
,…14分
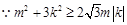 ,
,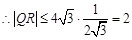 .
.
当且仅当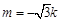 时,
时,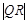 取最大值2,此时直线
取最大值2,此时直线 的方程为
的方程为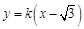 ,过焦点
,过焦点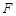 .
.
方法二:设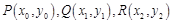 ,则直线
,则直线 的方程为
的方程为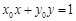 . ……11分
. ……11分
由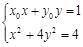 ,消
,消 得
得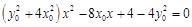 ,
,
则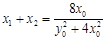 ,
,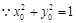 ,
,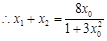 ,
,
由(1)知,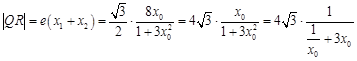 ,……14分
,……14分
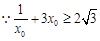 ,
,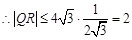 ,
,
当且仅当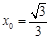 时,
时,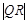 取最大值2,此时
取最大值2,此时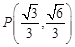 ,直线
,直线 过焦点
过焦点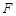 .
.
方法三:由(1)同理可求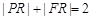 ,则
,则 ,………11分
,………11分
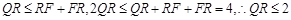 ,
,
当且仅当直线 过焦点
过焦点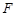 时等号成立,从而
时等号成立,从而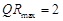 .
.
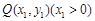 ,先利用焦半径公式表示
,先利用焦半径公式表示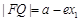 ,然后再想法求出|PQ|,也用x1表示出来.相加即可.
,然后再想法求出|PQ|,也用x1表示出来.相加即可.(2)根据离心率可求出a值,进而椭圆方程确定,然后设直线
 的方程为
的方程为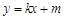 ,由直线QR与圆O相切,进而得到
,由直线QR与圆O相切,进而得到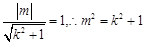 ,
,然后直线与椭圆方程联立,消y之后,表示出
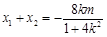 ,
,则
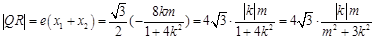 ,
,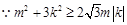 ,
,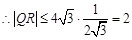 ,因而确定当且仅当
,因而确定当且仅当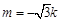 时,
时,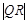 取最大值2.
取最大值2.(1)设
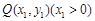 ,得
,得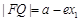 ,…………………3分
,…………………3分由
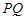 是圆
是圆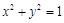 的切线,
的切线,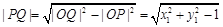 ,
,注意到
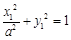 ,
,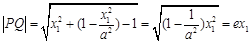 ,……………6分
,……………6分所以
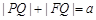 . ……………7分
. ……………7分(2)由题意,
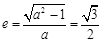 ,
,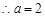 . …………………………9分
. …………………………9分方法一:设直线
 的方程为
的方程为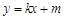 ,
,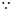 点
点 在第一象限,
在第一象限,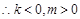 .
.由直线
 与圆
与圆 相切,
相切,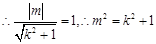 . …………………………11分
. …………………………11分由
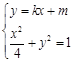 ,消
,消 得
得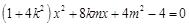 ,
,设
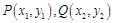 ,则
,则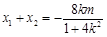 .
.由(1)知,
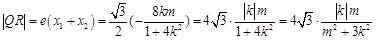 ,…14分
,…14分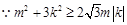 ,
,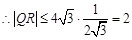 .
.当且仅当
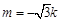 时,
时,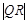 取最大值2,此时直线
取最大值2,此时直线 的方程为
的方程为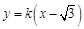 ,过焦点
,过焦点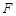 .
.方法二:设
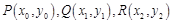 ,则直线
,则直线 的方程为
的方程为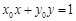 . ……11分
. ……11分由
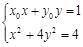 ,消
,消 得
得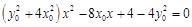 ,
,则
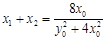 ,
,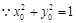 ,
,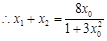 ,
,由(1)知,
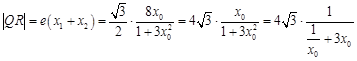 ,……14分
,……14分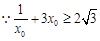 ,
,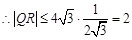 ,
,当且仅当
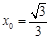 时,
时,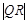 取最大值2,此时
取最大值2,此时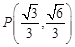 ,直线
,直线 过焦点
过焦点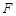 .
. 方法三:由(1)同理可求
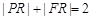 ,则
,则 ,………11分
,………11分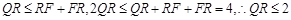 ,
,当且仅当直线
 过焦点
过焦点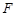 时等号成立,从而
时等号成立,从而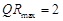 .
.
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目

 的离心率为
的离心率为 ,两焦点之间的距离为4.
,两焦点之间的距离为4.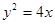 于A、B两点,
于A、B两点, 定点
定点 ,点
,点 为圆
为圆 上的动点,点
上的动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 。
。 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由。
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由。 :
: 的右焦点与抛物线
的右焦点与抛物线 的焦点相同,且
的焦点相同,且 的离心率
的离心率 ,又
,又 为椭圆的左右顶点,
为椭圆的左右顶点, 其上任一点(异于
其上任一点(异于 交直线
交直线 于点
于点 ,过
,过 作直线
作直线 的垂线交
的垂线交 轴于点
轴于点 ,求
,求 在直线
在直线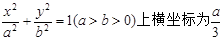 的点到左焦点的距离大于它到右准线的距离,则椭圆离心率e的取值范围是 .
的点到左焦点的距离大于它到右准线的距离,则椭圆离心率e的取值范围是 .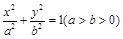 的左顶点与上顶点,椭圆的离心率
的左顶点与上顶点,椭圆的离心率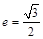 ,F1、F2为椭圆的左、右焦点,点P是线段AD上的任一点,且
,F1、F2为椭圆的左、右焦点,点P是线段AD上的任一点,且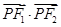 的最大值为1 .
的最大值为1 . OB(O为坐标原点),若存在,求出该圆的方程;若不存在,请说明理由;
OB(O为坐标原点),若存在,求出该圆的方程;若不存在,请说明理由;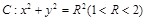 相切于A1,且l与椭圆E有且仅有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
相切于A1,且l与椭圆E有且仅有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.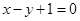 经过椭圆S:
经过椭圆S: 的一个焦点和一个顶点.
的一个焦点和一个顶点. 轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.
轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k. ,求证:
,求证: .
.
 上存在一点P,使得它对两个焦点
上存在一点P,使得它对两个焦点 ,
, 的张角
的张角 ,则该椭圆的离心率的取值范围是
,则该椭圆的离心率的取值范围是



 的曲线恰好有两个不同的公共点,则实数
的曲线恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是

