题目内容
定义在R上的函数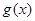 及二次函数
及二次函数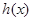 满足:
满足: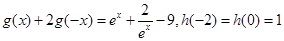 且
且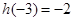 .
.
(1)求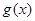 和
和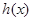 的解析式;
的解析式;
(2)对于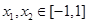 ,均有
,均有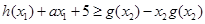 成立,求
成立,求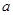 的取值范围;
的取值范围;
(3)设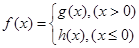 ,讨论方程
,讨论方程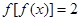 的解的个数情况.
的解的个数情况.
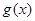 及二次函数
及二次函数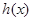 满足:
满足: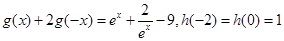 且
且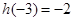 .
.(1)求
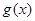 和
和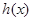 的解析式;
的解析式;(2)对于
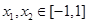 ,均有
,均有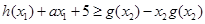 成立,求
成立,求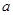 的取值范围;
的取值范围;(3)设
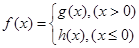 ,讨论方程
,讨论方程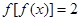 的解的个数情况.
的解的个数情况.(1)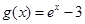 ,
,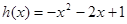 ;(2)
;(2)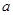 的取值范围为
的取值范围为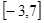 ;(3)
;(3)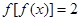 有5个解.
有5个解.
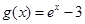 ,
,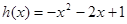 ;(2)
;(2)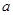 的取值范围为
的取值范围为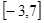 ;(3)
;(3)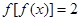 有5个解.
有5个解.试题分析:(1)根据已知的函数方程
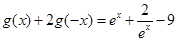 ,可以得到
,可以得到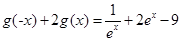 ,联立已知条件的函数方程,即可解得
,联立已知条件的函数方程,即可解得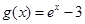 ,又由条件二次函数
,又由条件二次函数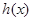 及
及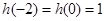 ,可设
,可设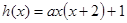 ,再根据
,再根据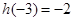 ,可求得
,可求得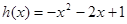 ;(2)问题等价于求使
;(2)问题等价于求使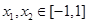 ,
,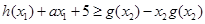 恒成立的
恒成立的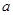 的取值范围,即求当
的取值范围,即求当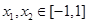 ,
,使
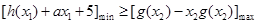 成立的
成立的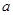 的取值范围,通过判断
的取值范围,通过判断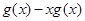 的单调性可知,其在
的单调性可知,其在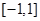 上单调递增,因此只需
上单调递增,因此只需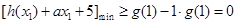 ,由(1)求得的二次函数
,由(1)求得的二次函数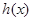 的解析式,可得只需
的解析式,可得只需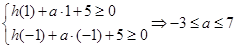 ,即
,即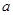 的取值范围为
的取值范围为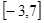 ;(3)根据条件及(1),(2)所求得的解析式,可画出
;(3)根据条件及(1),(2)所求得的解析式,可画出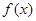 的示意图,根据示意图,可以得到方程
的示意图,根据示意图,可以得到方程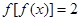 即等价于
即等价于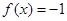 或
或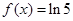 ,再从
,再从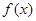 示意图上可得:
示意图上可得: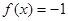 有2个解,
有2个解, 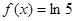 有
有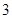 个解,因此
个解,因此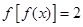 有
有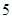 个解.
个解.试题解析:(1)
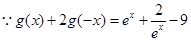 ,①
,①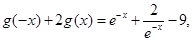 即
即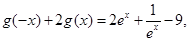 ②
②由①②联立解得:
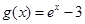 . 2分,
. 2分,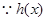 是二次函数, 且
是二次函数, 且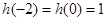 ,可设
,可设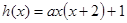 ,
,由
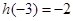 ,解得
,解得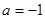 .∴
.∴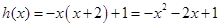 ,
,∴
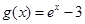 ,
,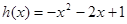 5分;
5分;(2)设
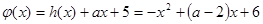 ,
,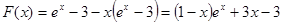 ,
,依题意知:当
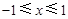 时,
时, 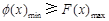
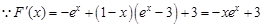 ,在
,在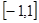 上单调递减,
上单调递减,∴
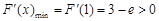 7分
7分∴
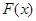 在
在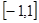 上单调递增,,∴
上单调递增,,∴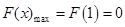
∴
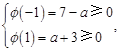 解得:
解得: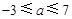 ,
,∴实数
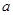 的取值范围为
的取值范围为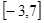 . 10分;
. 10分;由题意,可画出
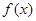 的示意图如图所示:
的示意图如图所示: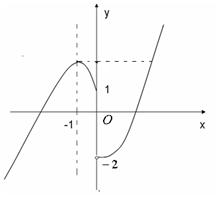
令
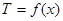 ,则
,则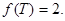
∴
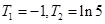 ,由示意图可知:
,由示意图可知: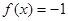 有2个解,
有2个解, 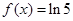 有
有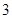 个解.
个解.∴
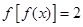 有
有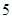 个解. 14分.
个解. 14分. 
练习册系列答案
相关题目
 .
.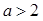 ,求
,求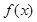 在
在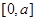 上的最大值.
上的最大值.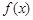 在
在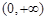 上为减函数,且
上为减函数,且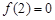 ,则不等式
,则不等式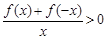 的解集为( ).
的解集为( ).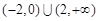
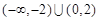
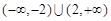
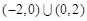
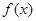 是定义在
是定义在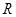 上的奇函数,且
上的奇函数,且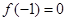 ,若不等式
,若不等式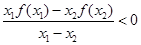 对区间
对区间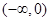 内任意的两个不相等的实数
内任意的两个不相等的实数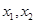 都成立,则不等式
都成立,则不等式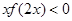 的解集是 。
的解集是 。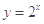
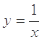
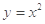
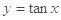
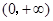 上单调递增的是( )
上单调递增的是( )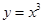
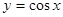
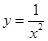
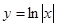
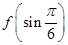 <
<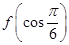 ;②f(sin l)>f(cos l);
;②f(sin l)>f(cos l);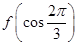 <
<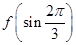 ;④f(cos 2)>f(sin 2).
;④f(cos 2)>f(sin 2).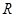 上的奇函数
上的奇函数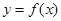 在
在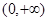 上单调递增,且
上单调递增,且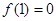 ,则不等式
,则不等式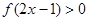 的解集为 .
的解集为 .