Question

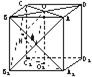如图，在棱长为a的正方体ABCD-A₁B₁C₁D₁中，M、O、O₁分别是A₁B、AC、A₁C₁的中点，且OH⊥O₁B，垂足为H．
（1）求证：MO∥平面BB₁C₁C；
（2）分别求MO与OH的长；
（3）MO与OH是否为异面直线A₁B与AC的公垂线？为什么？求这两条异面直线间的距离．

Answer 1

分析：（1）要求证：MO∥平面BB₁C₁C，只需证明MO∥B₁C即可．
（2）直接求MO，在三角形中求OH的长；
（3）说明OH与异面直线A₁B与AC都垂直相交；求出MO与AC所成的角可以判断是否是公垂线，求这两条异面直线间的距离．由（2）可知结果．

解答：（1）证明：连接B₁C，∵MO是△AB₁C的中位线，∴MO∥B₁C．∵B₁C不在平面BB₁C₁C，
∴MO∥平面BB₁C₁C．
（2）解：MO=

1

2

B₁C=

2

2

a，
∵OH是Rt△BOO₁斜边上的高，BO=

2

2

a，
∴OH=

3

3

a．
（3）解：MO不是A₁B与AC的公垂线，MO∥B₁C，△AB₁C为正三角形，∴MO与AC成60°角．
∵AC⊥BD，AC⊥OO₁，∴AC⊥面BOO₁．∵OH不在面BOO₁内，∴OH⊥AC，OH⊥A₁C₁．
∵OH⊥O₁B，A₁C₁∩O₁B=O₁，∴OH⊥面BA₁C₁，OH⊥A₁B．∴OH是异面直线A₁B与AC的公垂线，
其长度即为这两条异面直线的距离．∴OH=

3

3

a．

点评：本题考查直线与平面的平行，直线与直线垂直，求距离问题，考查学生逻辑思维能力，空间想象能力，是中档题．