题目内容
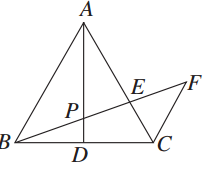
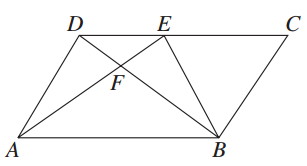
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,求证:PB2=PE·PF.

见解析
证明:连接PC,易证PC=PB,∠ABP=∠ACP.

∵CF∥AB,∴∠F=∠ABP,从而∠F=∠ACP.
又∠EPC为△CPE与△FPC的公共角,
从而△CPE∽△FPC,∴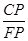 =
=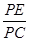 ,
,
∴PC2=PE·PF.
又PC=PB,∴PB2=PE·PF.

∵CF∥AB,∴∠F=∠ABP,从而∠F=∠ACP.
又∠EPC为△CPE与△FPC的公共角,
从而△CPE∽△FPC,∴
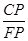 =
=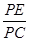 ,
,∴PC2=PE·PF.
又PC=PB,∴PB2=PE·PF.

练习册系列答案
相关题目
 的直径
的直径 ,
, 是
是 延长线上一点,
延长线上一点, ,割线
,割线 交圆
交圆 ,
, ,过点
,过点 的垂线,交直线
的垂线,交直线 于点
于点 ,交直线
,交直线 于点
于点 .
. ;
; 的值.
的值.
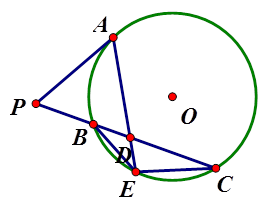
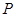 是
是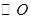 外一点,
外一点,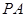 是切线,
是切线, 为切点,割线
为切点,割线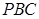 与
与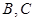 ,
,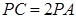 ,
,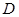 为
为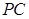 的中点,
的中点,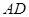 的延长线交
的延长线交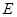 .证明:
.证明: ;
;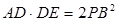


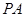 是圆
是圆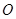 的切线,切点为
的切线,切点为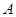 ,
,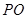 交圆
交圆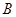 、
、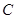 两点,且
两点,且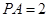 ,
,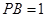 ,则
,则 的长为 .
的长为 .