题目内容
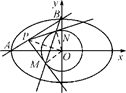
已知椭圆C: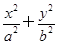 =1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=
=1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=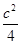 (c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
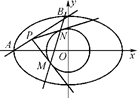
(1)若椭圆C经过两点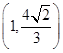 、
、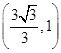 ,求椭圆C的方程;
,求椭圆C的方程;
(2)当c为定值时,求证:直线MN经过一定点E,并求 ·
·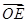 的值(O是坐标原点);
的值(O是坐标原点);
(3)若存在点P使得△PMN为正三角形,试求椭圆离心率的取值范围..
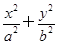 =1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=
=1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=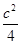 (c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(1)若椭圆C经过两点
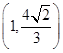 、
、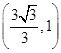 ,求椭圆C的方程;
,求椭圆C的方程;(2)当c为定值时,求证:直线MN经过一定点E,并求
 ·
·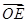 的值(O是坐标原点);
的值(O是坐标原点);(3)若存在点P使得△PMN为正三角形,试求椭圆离心率的取值范围..
(1) =1.(2)见解析(3)
=1.(2)见解析(3)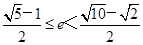
 =1.(2)见解析(3)
=1.(2)见解析(3)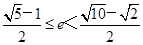
(1)解:令椭圆mx2+ny2=1,其中m=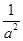 ,n=
,n=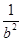 ,得
,得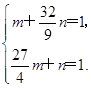 所以m=
所以m=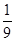 ,n=
,n=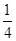 ,即椭圆方程为
,即椭圆方程为 =1.
=1.
(2)证明:直线AB: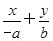 =1,设点P(x0,y0),则OP的中点为
=1,设点P(x0,y0),则OP的中点为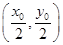 ,所以点O、M、P、N所在的圆的方程为
,所以点O、M、P、N所在的圆的方程为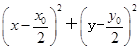 =
=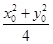 ,化简为x2-x0x+y2-y0y=0,与圆x2+y2=
,化简为x2-x0x+y2-y0y=0,与圆x2+y2=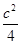 作差,即直线MN:x0x+y0y=
作差,即直线MN:x0x+y0y=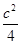 .
.
因为点P(x0,y0)在直线AB上,得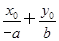 =1,
=1,
所以x0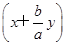 +
+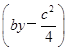 =0,即
=0,即
得x=-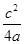 ,y=
,y=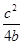 ,故定点E
,故定点E 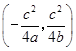 ,
, ·
·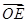 =
=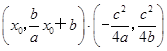 =
=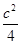 .
.
(3)解:由直线AB与圆G:x2+y2=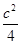 (c是椭圆的焦半距)相离,则
(c是椭圆的焦半距)相离,则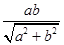 >
>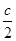 ,即4a2b2>c2(a2+b2),4a2(a2-c2)>c2(2a2-c2),得e4-6e2+4>0.因为0<e<1,所以0<e2<3-
,即4a2b2>c2(a2+b2),4a2(a2-c2)>c2(2a2-c2),得e4-6e2+4>0.因为0<e<1,所以0<e2<3-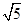 ①.连结ON、OM、OP,若存在点P使△PMN为正三角形,则在Rt△OPN中,OP=2ON=2r=c,所以
①.连结ON、OM、OP,若存在点P使△PMN为正三角形,则在Rt△OPN中,OP=2ON=2r=c,所以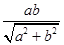 ≤c,a2b2≤c2(a2+b2),a2(a2-c2)≤c2(2a2-c2),得e4-3e2+1≤0.因为0<e<1,所以
≤c,a2b2≤c2(a2+b2),a2(a2-c2)≤c2(2a2-c2),得e4-3e2+1≤0.因为0<e<1,所以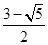 ≤e2<1,②.由①②得
≤e2<1,②.由①②得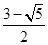 ≤e2<3-
≤e2<3-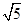 ,所以
,所以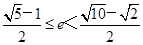
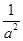 ,n=
,n=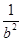 ,得
,得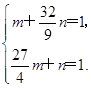 所以m=
所以m=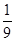 ,n=
,n=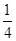 ,即椭圆方程为
,即椭圆方程为 =1.
=1.(2)证明:直线AB:
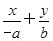 =1,设点P(x0,y0),则OP的中点为
=1,设点P(x0,y0),则OP的中点为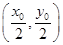 ,所以点O、M、P、N所在的圆的方程为
,所以点O、M、P、N所在的圆的方程为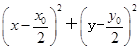 =
=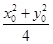 ,化简为x2-x0x+y2-y0y=0,与圆x2+y2=
,化简为x2-x0x+y2-y0y=0,与圆x2+y2=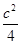 作差,即直线MN:x0x+y0y=
作差,即直线MN:x0x+y0y=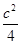 .
.
因为点P(x0,y0)在直线AB上,得
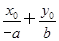 =1,
=1,所以x0
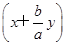 +
+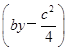 =0,即
=0,即
得x=-
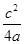 ,y=
,y=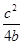 ,故定点E
,故定点E 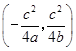 ,
, ·
·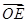 =
=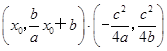 =
=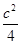 .
.(3)解:由直线AB与圆G:x2+y2=
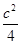 (c是椭圆的焦半距)相离,则
(c是椭圆的焦半距)相离,则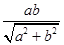 >
>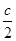 ,即4a2b2>c2(a2+b2),4a2(a2-c2)>c2(2a2-c2),得e4-6e2+4>0.因为0<e<1,所以0<e2<3-
,即4a2b2>c2(a2+b2),4a2(a2-c2)>c2(2a2-c2),得e4-6e2+4>0.因为0<e<1,所以0<e2<3-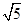 ①.连结ON、OM、OP,若存在点P使△PMN为正三角形,则在Rt△OPN中,OP=2ON=2r=c,所以
①.连结ON、OM、OP,若存在点P使△PMN为正三角形,则在Rt△OPN中,OP=2ON=2r=c,所以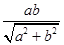 ≤c,a2b2≤c2(a2+b2),a2(a2-c2)≤c2(2a2-c2),得e4-3e2+1≤0.因为0<e<1,所以
≤c,a2b2≤c2(a2+b2),a2(a2-c2)≤c2(2a2-c2),得e4-3e2+1≤0.因为0<e<1,所以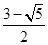 ≤e2<1,②.由①②得
≤e2<1,②.由①②得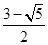 ≤e2<3-
≤e2<3-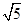 ,所以
,所以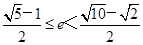

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 的抛物线
的抛物线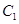 的焦点
的焦点 与椭圆
与椭圆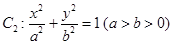 的右焦点重合,
的右焦点重合,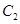 在第一和第四象限的交点分别为
在第一和第四象限的交点分别为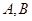 .
.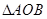 是边长为
是边长为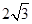 的正三角形,求抛物线
的正三角形,求抛物线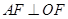 ,求椭圆
,求椭圆 .
.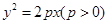 的焦点为
的焦点为 ,点
,点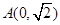 ,线段
,线段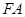 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线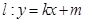 与抛物线相切于点
与抛物线相切于点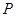 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以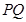 为直径的圆记为圆
为直径的圆记为圆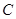 .
.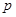 的值;
的值;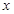 轴的位置关系;
轴的位置关系;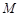 ,使得圆
,使得圆 的曲线即为函数
的曲线即为函数 的图象,对于函数
的图象,对于函数 上是单调递减函数;②函数
上是单调递减函数;②函数 对称;
对称; 至少存在一个零点.
至少存在一个零点.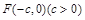 是双曲线
是双曲线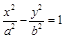 的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆
的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆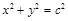 交于点P,且点P在抛物线
交于点P,且点P在抛物线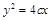 上,则e2 =( )
上,则e2 =( )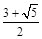
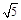
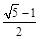
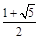
 +
+ =1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
=1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.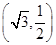 ,离心率是
,离心率是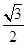 .
.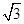 ,1)到两焦点的距离之和为4
,1)到两焦点的距离之和为4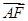 =3
=3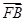 .求过O,A,B三点的圆的方程.
.求过O,A,B三点的圆的方程.