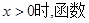题目内容
已知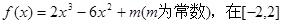 上有最大值为3,则f(x)在[-2,2]上的最小值为
上有最大值为3,则f(x)在[-2,2]上的最小值为
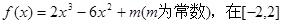 上有最大值为3,则f(x)在[-2,2]上的最小值为
上有最大值为3,则f(x)在[-2,2]上的最小值为| A.-5 | B.-11 | C.-29 | D.-37 |
D
先求一阶导数
f′(x)=6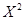 -12x
-12x
然后通过一阶导数看原函数增减性
f"(x)=6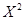 -12x>0为增函数,即x<0或x>2时,原函数递增;0<x<2时,原函数递减。
-12x>0为增函数,即x<0或x>2时,原函数递增;0<x<2时,原函数递减。
接下来通过二阶导数求拐点
f′′(x)=12x-12
令f′′(x′)=12x′-12=0,得x′=1,即为拐点。
当x>1时,f′′(x)>0,曲线是凹的;当x<1时,f′′(x)<0,曲线是凸的。
现在可画出大致图形。
所以最大值为x=0,代入原函数为x=0时取最大值3,即m=3.
最小值可能为x=2,或x=-2,代入原函数比较得x=-2,为最小值,且最小值为-37。
f′(x)=6
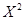 -12x
-12x然后通过一阶导数看原函数增减性
f"(x)=6
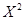 -12x>0为增函数,即x<0或x>2时,原函数递增;0<x<2时,原函数递减。
-12x>0为增函数,即x<0或x>2时,原函数递增;0<x<2时,原函数递减。接下来通过二阶导数求拐点
f′′(x)=12x-12
令f′′(x′)=12x′-12=0,得x′=1,即为拐点。
当x>1时,f′′(x)>0,曲线是凹的;当x<1时,f′′(x)<0,曲线是凸的。
现在可画出大致图形。
所以最大值为x=0,代入原函数为x=0时取最大值3,即m=3.
最小值可能为x=2,或x=-2,代入原函数比较得x=-2,为最小值,且最小值为-37。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
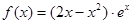 判断正确的是( )
判断正确的是( )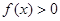 的解集是
的解集是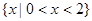 ;
;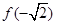 是极小值,
是极小值,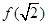 是极大值;
是极大值;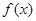 没有最小值,也没有最大值.
没有最小值,也没有最大值.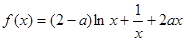 (a∈R).
(a∈R).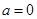 时,求
时,求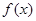 的极值;
的极值;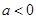 时,求
时,求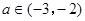 及
及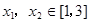 ,恒有
,恒有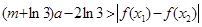
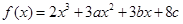 在
在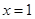 及
及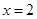 时取得极值.
时取得极值.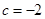 时,求函数
时,求函数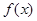 在区间
在区间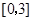 上的最大值.
上的最大值.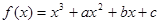 ,当
,当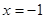 时,
时,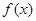 的极大值为7;当
的极大值为7;当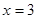 时,
时,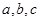 的值; (2)函数
的值; (2)函数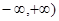 内存在极值,则( )
内存在极值,则( )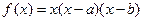 。
。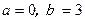 ,函数
,函数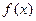 在
在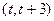 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求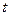 的取值范围;
的取值范围;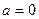 时,
时,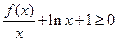 对任意的
对任意的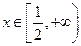 恒成立,求
恒成立,求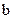 的取值范围;
的取值范围;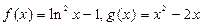
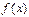 的单调区间与极值;
的单调区间与极值; 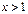 时,比较
时,比较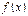 与
与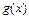 的大小.
的大小.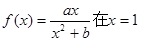 处取得极值2,则当
处取得极值2,则当