题目内容
(6分)已知函数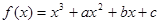 ,当
,当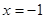 时,
时,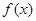 的极大值为7;当
的极大值为7;当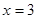 时,
时,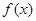 有极小值.求(1)
有极小值.求(1)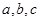 的值; (2)函数
的值; (2)函数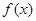 的极小值.
的极小值.
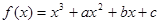 ,当
,当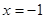 时,
时,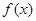 的极大值为7;当
的极大值为7;当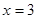 时,
时,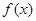 有极小值.求(1)
有极小值.求(1)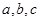 的值; (2)函数
的值; (2)函数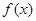 的极小值.
的极小值.(1)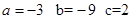 (2)
(2)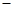 25
25
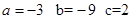 (2)
(2) 25
25解:f(x)=x3+ax2+bx+c,f′(x)=3x2+2ax+6,
∵x=-1时函数取得极大值,x=3时函数取得极小值,
∴-1,3是方程f′(x)=0的根,即为方程3x2+2ax+b="0" 的两个根,
由一元二次方程根与系数的关系有
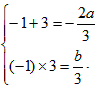 ,
,∴
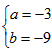
∴f(x)=x3-3x2-9x+c,
∵x=-1时取得极大值7,
∴(-1)3-3(-1)2-9(-1)+c=7,
∴c=2,
∴函数f(x)的极小值为f(3)=33-3×32-9×3+2=-25。

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
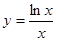 的最大值为( )
的最大值为( )



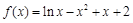 .
.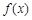 的单调区间;
的单调区间;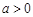 ,求
,求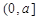 上的最大值;
上的最大值;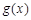
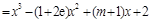 ,(
,(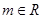 ),试讨论函数
),试讨论函数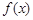 与
与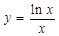 的最大值为( )
的最大值为( )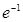



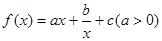 的图象在点(1,
的图象在点(1,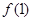 )处的切线方程为
)处的切线方程为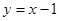 。
。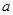 表示出
表示出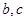 ;
;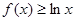 在[1,+∞)上恒成立,求
在[1,+∞)上恒成立,求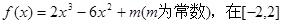 上有最大值为3,则f(x)在[-2,2]上的最小值为
上有最大值为3,则f(x)在[-2,2]上的最小值为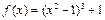 的极值是 ( )
的极值是 ( )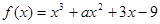 ,已知
,已知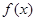 在
在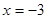 时取得极值,则
时取得极值,则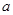 = ▲ .
= ▲ .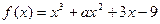 ,已知
,已知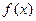 在
在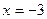 时取得极值,则
时取得极值,则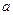 = ▲ .
= ▲ .