题目内容
2.若高次不等式(-x3+x2+2x)(x2-1)≥0,则x的取值范围为( )| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,0]∪[1,2] | D. | [1,2] |
分析 用条件把原不等式转化为 x(x-2)(x-1)(x+1)2≤0,再用穿根法解不等式,求得它的解集.
解答  解:高次不等式(-x3+x2+2x)(x2-1)≥0,即 x(x2-x-2)(x+1)(x-1)≤0,
解:高次不等式(-x3+x2+2x)(x2-1)≥0,即 x(x2-x-2)(x+1)(x-1)≤0,
即 x(x-2)(x-1)(x+1)2≤0,用穿根法求得它的解集为{x|x≤0或1≤x≤2},
故选:C.
点评 本题主要用穿根法解高次不等式,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.“x=1”是“x2-1=0”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
10.设a,b∈R,则“a=0”是“ab=0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
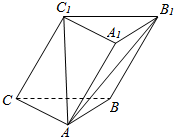 如图,三棱柱ABC-A1B1C1的侧棱与底面成60°角,侧棱长与底面边长均相等,侧面B1C1CB⊥面ABC.
如图,三棱柱ABC-A1B1C1的侧棱与底面成60°角,侧棱长与底面边长均相等,侧面B1C1CB⊥面ABC.