题目内容
【题目】(1)已知双曲线的中心在原点,焦点在x轴上,实轴长为4,渐近线方程为![]() .求双曲线的标准方程;
.求双曲线的标准方程;
(2)过(1)中双曲线上一点P的直线分别交两条渐近于![]() 两点,且P是线段AB的中点,求证:
两点,且P是线段AB的中点,求证:![]() 为常数;
为常数;
(3)我们知道函数![]() 的图象是由双曲线
的图象是由双曲线![]() 的图象逆时针旋转45°得到的,函数
的图象逆时针旋转45°得到的,函数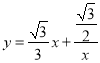 的图象也是双曲线,请尝试写出曲线
的图象也是双曲线,请尝试写出曲线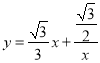 的性质(不必证明).
的性质(不必证明).
【答案】(1)![]() (2)证明见解析(3)详见解析
(2)证明见解析(3)详见解析
【解析】
(1)根据双曲线的性质求得双曲线的方程;
(2)方法一:设A,B点坐标,求得P点坐标,代入双曲线方程,即可求得![]() ;
;
方法二:分类讨论,设直线AB的方程,分别求得A和B点坐标,求得P点坐标,代入双曲线方程,即可求得![]() ;
;
(3)根据曲线方程,分别求得曲线的性质.
(1)设双曲线的方程为![]() ,由
,由![]() ,
,
由双曲线的渐近线方程为![]() ,则
,则![]() ,则
,则![]() ,
,
∴双曲线的方程为:![]() ;
;
(2)法一:由题不妨设![]() ,则
,则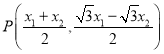 ,
,
则P在双曲线上,代入双曲线方程得![]()
法二:当直线AB的斜率不存在时,显然![]() ,则
,则![]() ;
;
当直线AB的斜率存在时,设直线AB的方程为![]()
则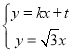 ,则
,则 ,
,
同理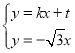 ,则
,则 ,
,
此时,![]() ,代入双曲线方程得
,代入双曲线方程得![]() ,则
,则![]()
(3)①对称中心:原点,对称轴方程:![]() ,
,
②顶点坐标为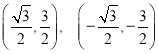 ,焦点坐标:
,焦点坐标:![]() ,
,![]() ,
,
实轴长:![]() ,虚轴长:2b=2,焦距:2c=4;
,虚轴长:2b=2,焦距:2c=4;
③范围:x≠0,![]() ,
,
④渐近线:![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目