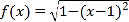题目内容
【题目】如图,一个角形海湾![]() (常数
(常数![]() 为锐角).拟用长度为
为锐角).拟用长度为![]() (
(![]() 为常数)的围网围成一个养殖区,有以下两种方案可供选择:方案一:如图1,围成扇形养殖区
为常数)的围网围成一个养殖区,有以下两种方案可供选择:方案一:如图1,围成扇形养殖区![]() ,其中
,其中![]() ;方案二:如图2,围成三角形养殖区
;方案二:如图2,围成三角形养殖区![]() ,其中
,其中![]() .
.
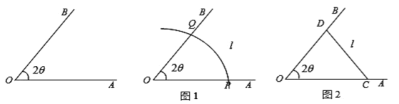
(1)求方案一中养殖区的面积![]() ;
;
(2)求方案二中养殖区的最大面积(用![]() 表示);
表示);
(3)为使养殖区的面积最大,应选择何种方案?并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)应选择方案一.
;(3)应选择方案一.
【解析】
(1)设此扇形所在的圆的半径为![]() ,则
,则![]() ,可得
,可得![]() .利用扇形面积计算公式可得
.利用扇形面积计算公式可得![]() .
.
(2)设![]() ,
,![]() ,利用余弦定理与基本不等式的性质可得:
,利用余弦定理与基本不等式的性质可得:![]() ,可得:
,可得:![]() ,即可得出.
,即可得出.
(3)由于![]() ,令
,令![]() ,求导,可得
,求导,可得![]() 在
在![]() 上单调递增.即可得出结论.
上单调递增.即可得出结论.
(1)设![]() ,则
,则![]() ,即
,即![]() ,所以
,所以
![]() .
.
(2)设![]() .由余弦定理,得
.由余弦定理,得![]() ,所以
,所以
![]() .
.
所以![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
所以![]() ,即
,即![]() .
.
(3)![]() ,
,
令![]() ,则
,则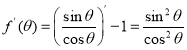 .
.
当![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增.
上单调递增.
所以,当![]() 时,总有
时,总有![]() ,即
,即![]() ,即
,即![]() .
.
答:为使养殖区面积最大,应选择方案一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目