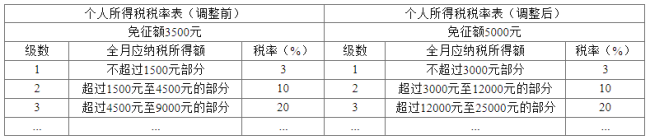
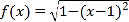题目内容
【题目】已知定义域为![]() 的函数
的函数![]() 满足:(1)对任意
满足:(1)对任意![]() ,恒有
,恒有![]() 成立;(2)当
成立;(2)当![]() 时,
时,![]() .给出如下结论:
.给出如下结论:
①对任意![]() ,有
,有![]() ;
;
②函数![]() 的值域为
的值域为![]()
③存在![]() ,使得
,使得![]() ;
;
④“函数![]() 在区间
在区间![]() 上单调递减”的充要条件是“存在
上单调递减”的充要条件是“存在![]() ,使得
,使得![]() ”.
”.
上述结论正确有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
依据题中条件注意研究每个选项的正确性,连续利用题中第(1)个条件得到①正确;连续利用题中第(2)个条件得到②正确;利用反证法及2x变化如下:2,4,8,16,32,判断③命题错误;据①②③的正确性可得④是正确的.
①f(2m)=f(22m﹣1)=2f(2m﹣1)=…=2m﹣1f(2),正确;
②取x∈(2m,2m+1],则![]() ∈(1,2];f(
∈(1,2];f(![]() )=2
)=2![]() ,从而
,从而
f(x)=2f(![]() )=…=2mf(
)=…=2mf(![]() )=2m+1﹣x,其中,m=0,1,2,…
)=2m+1﹣x,其中,m=0,1,2,…
从而f(x)∈[0,+∞),正确;
③f(2n+1)=2n+1﹣2n﹣1,假设存在n使f(2n+1)=9,即存在x1,x2,![]() 10,又,2x变化如下:2,4,8,16,32,显然不存在,所以该命题错误;
10,又,2x变化如下:2,4,8,16,32,显然不存在,所以该命题错误;
④根据前面的分析容易知道该选项正确;
综合有正确的序号是①②④.
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目