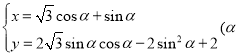题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 是函数
是函数![]() 的一个极值点,求实数
的一个极值点,求实数![]() 的值及
的值及![]() 在
在![]() 内的最小值;
内的最小值;
(Ⅱ)当![]() 时,求证:函数
时,求证:函数![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析
;(Ⅱ)见解析
【解析】
(Ⅰ)由已知条件的导函数,以及![]() ,从而求出实数
,从而求出实数![]() 的值,利用导数求出函数
的值,利用导数求出函数![]() 在
在![]() 内的单调性,从而得到
内的单调性,从而得到![]() 在
在![]() 内的最小值
内的最小值
(Ⅱ)由题可得![]() ,令
,令![]() ,要证函数
,要证函数![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,即证
,即证![]() 只有唯一根,利用导数求出
只有唯一根,利用导数求出![]() 的单调区间与值域即可,且由零点定理可知
的单调区间与值域即可,且由零点定理可知![]() ,由
,由![]() ,可得
,可得![]() ,代入
,代入![]() 中,利用导数求出
中,利用导数求出![]() 在
在![]() 内的最值即可证明
内的最值即可证明![]() 。
。
(Ⅰ)由题可得:![]() ,则
,则![]() ,
,
![]()
![]() 是函数
是函数![]() 的一个极值点,
的一个极值点,
![]()
![]() ,即
,即![]() ,解得:
,解得:![]() ,经检验,当
,经检验,当![]() 时,
时,![]() 是函数
是函数![]() 的一个极值点;
的一个极值点;
![]() ;
;
当![]() 时,
时,![]()
![]() ,令
,令![]() ,解得:
,解得:![]() 或
或![]() ,
,
当![]() 时,
时,![]() 、
、![]() 的变化如下表:
的变化如下表:
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
所以当![]() 时,
时,![]() 有最小值,
有最小值,![]()
(Ⅱ)当![]() 时,
时,![]() ,
,
![]()
![]()
令![]() ,
,![]() ,则
,则![]() ,
,
由于![]() 恒成立,所以
恒成立,所以![]() 恒大于零,则
恒大于零,则![]() 在
在![]() 上单调递增,
上单调递增,
由于![]() ,
,![]() ,根据零点定理,可得存在唯一的
,根据零点定理,可得存在唯一的![]() ,使得
,使得![]() ,
,
![]() 令
令![]() ,解得:
,解得:![]() ,
,![]() ,当
,当![]() 或
或![]() 时,
时,![]() ,即
,即![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() 的单调减区间为
的单调减区间为![]() ,
,
![]() 函数
函数![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() ,
,![]() ,则
,则![]() ;
;
![]()
![]()
![]() ,
,
则![]() ,令
,令![]() ,解得:
,解得:![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,
,![]() ,所以
,所以![]()

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】汽车“定速巡航”技术是用于控制汽车的定速行驶,当汽车被设定为定速巡航状态时,电脑根据道路状况和汽车的行驶阻力自动控制供油量,使汽车始终保持在所设定的车速行驶,而无需司机操纵油门,从而减轻疲劳,促进安全,节省燃料.某汽车公司为测量某型号汽车定速巡航状态下的油耗情况,选择一段长度为240km的平坦高速路段进行测试.经多次测试得到一辆汽车每小时耗油量F(单位:L)与速度v(单位:km/h)(![]() )的下列数据:
)的下列数据:
v | 0 | 40 | 60 | 80 | 120 |
F | 0 |
|
| 10 | 20 |
为了描述汽车每小时耗油量与速度的关系,现有以下三种函数模型供选择:
![]() ,
, ,
,![]() .
.
(1)请选出你认为最符合实际的函数模型,并求出相应的函数解析式.
(2)这辆车在该测试路段上以什么速度行驶才能使总耗油量最少?