题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的最小值及
的最小值及![]() 取到最小值时自变量x的集合;
取到最小值时自变量x的集合;
(2)指出函数y=![]() 的图象可以由函数y=sinx的图象经过哪些变换得到;
的图象可以由函数y=sinx的图象经过哪些变换得到;
(3)当x∈[0,m]时,函数y=f(x)的值域为![]() ,求实数m的取值范围.
,求实数m的取值范围.
【答案】(1) ![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3) ![]() .
.
【解析】
(1)利用正弦函数的性质求出最小值以及取到最小值时自变量x的集合;
(2)由正弦函数的相位变换、周期变换、振幅变换描述即可;
(3)画出函数![]() 的图像,根据图像找到值域为
的图像,根据图像找到值域为![]() 的图像,即可确定实数m的取值范围.
的图像,即可确定实数m的取值范围.
(1)![]() ,此时
,此时![]() ,即
,即![]() ,
,
即此时自变量x的集合是![]() .
.
(2)把函数y=sinx的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,再把函数
的图象,再把函数![]() 的图象上所有点的纵坐标不变,横坐标缩短为原来的
的图象上所有点的纵坐标不变,横坐标缩短为原来的![]() ,得到函数
,得到函数![]() 的图象,最后再把函数
的图象,最后再把函数![]() 的图象上所有点的横坐标不变,纵坐标伸长为原来的2倍,得到函数
的图象上所有点的横坐标不变,纵坐标伸长为原来的2倍,得到函数![]() 的图象.
的图象.
(3)如图,因为当x∈[0,m]时,y=f(x)取到最大值2,所以![]() .
.
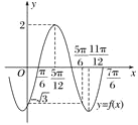
又函数y=f(x)在![]() 上是减函数,
上是减函数,
故m的最大值为![]() 内使函数值为
内使函数值为![]() 的值,
的值,
令![]() ,得
,得![]() ,所以m的取值范围是
,所以m的取值范围是![]() .
.

【题目】国家放开二胎政策后,不少家庭开始生育二胎,随机调查110名性别不同且为独生子女的高中生,其中同意生二胎的高中生占随机调查人数的![]() ,统计情况如下表:
,统计情况如下表:
同意 | 不同意 | 合计 | |
男生 |
| 20 | |
女生 | 20 |
| |
合计 | 110 |
(l)求![]() ,
,![]() 的值
的值
(2)根据以上数据,能否有99%的把握认为同意生二胎与性别有关?请说明理由.
附:![]()
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|