Question

【题目】在平面直角坐标系xOy中，动点P与两定点A（-2，0），B（2，0）连线的斜率之积为-，记点P的轨迹为曲线C

（I）求曲线C的方程；

（II）若过点（-，0）的直线l与曲线C交于M，N两点，曲线C上是否存在点E使得四边形OMEN为平行四边形？若存在，求直线l的方程，若不存在，说明理由

Answer 1

【答案】（Ⅰ）曲线C的方程为=1（x≠±2）（II）存在，直线l的方程为.

【解析】

（I）设动点为，直接把斜率之积为用坐标表示出来即可；

（II）假设存在符合条件的点，由题意知直线l的斜率不为零，同时设直线l的方程为，，把直线方程代入曲线方程，由韦达定理得，同时求得，而平行四边形存在，则有，从而可得点坐标，再代入（I）中所求曲线方程可求得参数值，说明假设正确．

解：（Ⅰ）设P（x,y）,有·=-

得·=-

整理得=1（x≠±2）

∴曲线C的方程为=1（x≠±2）

（II）假设存在符合条件的点E（）由题意知直线l的斜率不为零

设直线l的方程为x=my-

点M坐标为（）、点N坐标为（）

由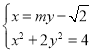得：（+2）-2my-2=0,△>0

∴+

则+=-

由四边形OMEN为平行四边形，得到

∴E（-）

把点E坐标代入曲线C的方程得：-4=0，解得

∴直线l的方程为