题目内容
13.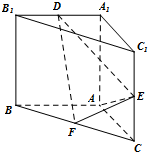 直三棱柱ABC-A1B1C1 中,AA1=AB=AC=1,E,F分别是CC1、BC 的中点,AE⊥
直三棱柱ABC-A1B1C1 中,AA1=AB=AC=1,E,F分别是CC1、BC 的中点,AE⊥A1B1,D为棱A1B1上的点.
(1)证明:DF⊥AE;
(2)是否存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为$\frac{\sqrt{14}}{14}$?若存在,说明点D的位置,若不存在,说明理由.
分析 (1)先证明AB⊥AC,然后以A为原点建立空间直角坐标系A-xyz,则能写出各点坐标,由$\overrightarrow{{A}_{1}D}$与$\overrightarrow{{A}_{1}{B}_{1}}$共线可得D(λ,0,1),所以$\overrightarrow{DF}$•$\overrightarrow{AE}$=0,即DF⊥AE;
(2)通过计算,面DEF的法向量为$\overrightarrow{n}$可写成$\overrightarrow{n}$=(3,1+2λ,2(1-λ)),又面ABC的法向量$\overrightarrow{m}$=(0,0,1),令|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=$\frac{\sqrt{14}}{14}$,解出λ的值即可.
解答 (1)证明:∵AE⊥A1B1,A1B1∥AB,∴AE⊥AB,
又∵AA1⊥AB,AA1⊥∩AE=A,∴AB⊥面A1ACC1,
又∵AC?面A1ACC1,∴AB⊥AC,
以A为原点建立如图所示的空间直角坐标系A-xyz,
则有A(0,0,0),E(0,1,$\frac{1}{2}$),F($\frac{1}{2}$,$\frac{1}{2}$,0),A1(0,0,1),B1(1,0,1),
设D(x,y,z),$\overrightarrow{{A}_{1}D}=λ\overrightarrow{{A}_{1}{B}_{1}}$ 且λ∈[0,1],即(x,y,z-1)=λ(1,0,0),
则 D(λ,0,1),所以$\overrightarrow{DF}$=($\frac{1}{2}-λ$,$\frac{1}{2}$,-1),
∵$\overrightarrow{AE}$=(0,1,$\frac{1}{2}$),∴$\overrightarrow{DF}$•$\overrightarrow{AE}$=$\frac{1}{2}-\frac{1}{2}$=0,所以DF⊥AE;
(2)结论:存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为$\frac{\sqrt{14}}{14}$.
理由如下:
设面DEF的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{FE}=0}\\{\overrightarrow{n}•\overrightarrow{DF}=0}\end{array}\right.$,
∵$\overrightarrow{FE}$=($-\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$),$\overrightarrow{DF}$=($\frac{1}{2}-λ$$\frac{1}{2}$,-1),
∴$\left\{\begin{array}{l}{-\frac{1}{2}x+\frac{1}{2}y+\frac{1}{2}z=0}\\{(\frac{1}{2}-λ)x+\frac{1}{2}y-z=0}\end{array}\right.$,即$\left\{\begin{array}{l}{x=\frac{3}{2(1-λ)}z}\\{y=\frac{1+2λ}{2(1-λ)}z}\end{array}\right.$,
令z=2(1-λ),则$\overrightarrow{n}$=(3,1+2λ,2(1-λ)).
由题可知面ABC的法向量$\overrightarrow{m}$=(0,0,1),
∵平面DEF与平面ABC所成锐二面角的余弦值为$\frac{\sqrt{14}}{14}$,
∴|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{14}}{14}$,即$\frac{|2(1-λ)|}{\sqrt{9+(1+2λ)^{2}+4(1-λ)^{2}}}$=$\frac{\sqrt{14}}{14}$,
解得$λ=\frac{1}{2}$或$λ=\frac{7}{4}$(舍),所以当D为A1B1中点时满足要求.
点评 本题考查空间中直线与直线的位置关系、空间向量及其应用,建立空间直角坐标系是解决问题的关键,属中档题.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案