题目内容
2.求使函数y=sin4x取得最大值的x的集合,并指出最大值是多少.分析 直接利用正弦型函数的性质来处理,利用整体思想求出自变量的值.
解答 解:函数y=sin4x的最大值为1.
当4x=2kπ+$\frac{π}{2}$(k∈Z),即x=$\frac{kπ}{2}+\frac{π}{8}$(k∈Z)时函数的最大值为1,
此时函数y=sin4x取得最大值的x的集合为:{x|x=$\frac{kπ}{2}+\frac{π}{8}$}(k∈Z).
点评 本题考查的知识要点:正弦型函数的性质的应用,及相关的运算问题.

练习册系列答案
相关题目
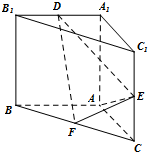 直三棱柱ABC-A1B1C1 中,AA1=AB=AC=1,E,F分别是CC1、BC 的中点,AE⊥
直三棱柱ABC-A1B1C1 中,AA1=AB=AC=1,E,F分别是CC1、BC 的中点,AE⊥