题目内容
已知椭圆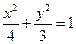 内的一点
内的一点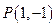 ,
,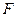 是椭圆的右焦点,在椭圆上求一点
是椭圆的右焦点,在椭圆上求一点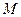 ,使
,使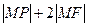 之值最小。
之值最小。
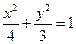 内的一点
内的一点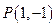 ,
,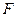 是椭圆的右焦点,在椭圆上求一点
是椭圆的右焦点,在椭圆上求一点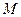 ,使
,使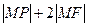 之值最小。
之值最小。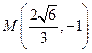
设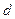 为
为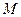 到右准线的距离,过
到右准线的距离,过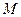 作准线的垂线,垂足为
作准线的垂线,垂足为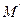 ,∵
,∵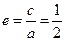 ,
,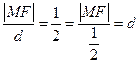 ,即
,即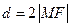 ,故
,故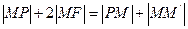 为最小,显然,当
为最小,显然,当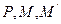 三点共线时为最小,从而求得
三点共线时为最小,从而求得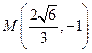 。
。
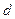 为
为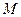 到右准线的距离,过
到右准线的距离,过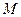 作准线的垂线,垂足为
作准线的垂线,垂足为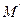 ,∵
,∵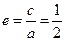 ,
,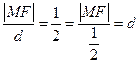 ,即
,即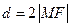 ,故
,故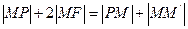 为最小,显然,当
为最小,显然,当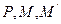 三点共线时为最小,从而求得
三点共线时为最小,从而求得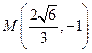 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
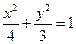 内的一点
内的一点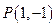 ,
,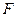 是椭圆的右焦点,在椭圆上求一点
是椭圆的右焦点,在椭圆上求一点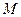 ,使
,使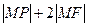 之值最小。
之值最小。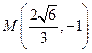
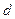 为
为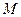 到右准线的距离,过
到右准线的距离,过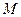 作准线的垂线,垂足为
作准线的垂线,垂足为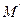 ,∵
,∵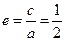 ,
,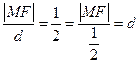 ,即
,即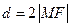 ,故
,故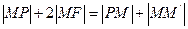 为最小,显然,当
为最小,显然,当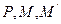 三点共线时为最小,从而求得
三点共线时为最小,从而求得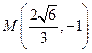 。
。
 阅读快车系列答案
阅读快车系列答案