题目内容


求证:
 到焦点F2的距离也成等差数列。
到焦点F2的距离也成等差数列。
证明:
设椭圆的一条准线方程为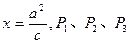 到准线的距离为
到准线的距离为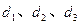
则根据椭圆的第二定义:

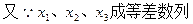
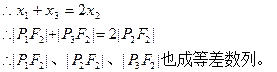
设椭圆的一条准线方程为
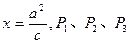 到准线的距离为
到准线的距离为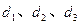
则根据椭圆的第二定义:


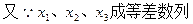
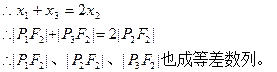
这道例题主要是对椭圆第二定义的应用,同时若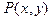 是椭圆上任一点,
是椭圆上任一点,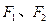 是椭圆的左、右焦点,则
是椭圆的左、右焦点,则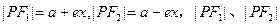 叫做椭圆的焦半径。
叫做椭圆的焦半径。
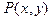 是椭圆上任一点,
是椭圆上任一点,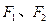 是椭圆的左、右焦点,则
是椭圆的左、右焦点,则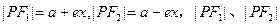 叫做椭圆的焦半径。
叫做椭圆的焦半径。
练习册系列答案
相关题目
题目内容


 到焦点F2的距离也成等差数列。
到焦点F2的距离也成等差数列。
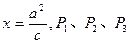 到准线的距离为
到准线的距离为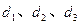


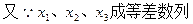
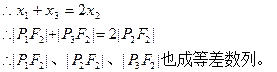
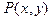 是椭圆上任一点,
是椭圆上任一点,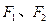 是椭圆的左、右焦点,则
是椭圆的左、右焦点,则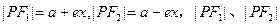 叫做椭圆的焦半径。
叫做椭圆的焦半径。