题目内容
设a,b,c均为正数,且a+b+c=1,证明:
(1)ab+bc+ca≤
(2) .
.
(1)ab+bc+ca≤

(2)
 .
.(1)见解析;
(2)见解析.
(2)见解析.
(1)由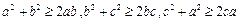 得
得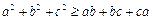 .
.
由题设得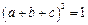 ,即
,即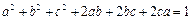 .
.
所以3(ab+bc+ca)≤1,即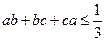 .
.
(2)因为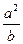 +b≥2a,
+b≥2a,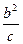 +c≥2b,
+c≥2b,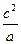 +a≥2c,故
+a≥2c,故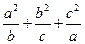 +(a+b+c)≥2(a+b+c),即
+(a+b+c)≥2(a+b+c),即
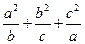 ≥a+b+c,所以
≥a+b+c,所以 .
.
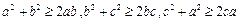 得
得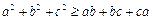 .
.由题设得
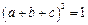 ,即
,即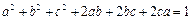 .
.所以3(ab+bc+ca)≤1,即
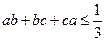 .
.(2)因为
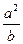 +b≥2a,
+b≥2a,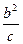 +c≥2b,
+c≥2b,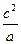 +a≥2c,故
+a≥2c,故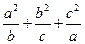 +(a+b+c)≥2(a+b+c),即
+(a+b+c)≥2(a+b+c),即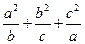 ≥a+b+c,所以
≥a+b+c,所以 .
.
练习册系列答案
相关题目
 ,
,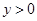 ,
, ,
, .求证
.求证 .
.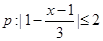 ,
,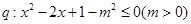 ,若
,若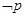 是
是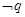 的充分不必要条件,求实数
的充分不必要条件,求实数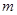 的取值范围.
的取值范围. 是两个实数,给出下列条件:①
是两个实数,给出下列条件:① ;②
;② ;③
;③ ;
; .其中能推出“
.其中能推出“ 的解集与不等式
的解集与不等式 的解集相同,则
的解集相同,则 的值为( )
的值为( )



 是定义在
是定义在 上的函数,若
上的函数,若 ,且对任意
,且对任意 ,满足
,满足 ,
, ,则
,则 =( )
=( )
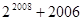


 的不等式
的不等式 的解集为
的解集为 ,则不等式
,则不等式 的解集为 .
的解集为 . =
= ”的证明过程:“等式两边同时乘以
”的证明过程:“等式两边同时乘以 得,左边=
得,左边= =
= =1,右边=1,左边=右边,故原不等式成立”,应用了
=1,右边=1,左边=右边,故原不等式成立”,应用了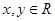 ,则
,则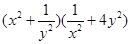 的最小值为 。
的最小值为 。