Question

1．如图所示，A，B，C是一条公路上的三点，BC=2AB=2km，从这三点分别观测一塔P，从A测得塔在北偏东60°，从B测得塔在正东，从C测得塔在南偏东60°，求该塔到这条公路的距离．

Answer 1

分析 过C，B，P分别作CMl，BNl，PQl，垂足分别为M，N，Q，设BN=x，可求PA，PC，由余弦定理可得AC²=PA²+PC²-2PA•PC•cos60°，解得x，过P作PD⊥AC，垂足为D，可求sin∠BAN=x，cos∠BAN=$\sqrt{1-{x}^{2}}$，sin∠CAP=$\frac{1}{2}$$\sqrt{1-{x}^{2}}$+$\frac{\sqrt{3}}{2}$x，由PD=APsin∠CAP即可求值得解．

解答 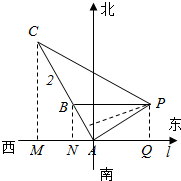解：如图所示，过C，B，P分别作CMl，BNl，PQl，垂足分别为M，N，Q，设BN=x，即PQ=x，PA=2x，
∵BC=2AB=2，
CM=3BN=3x，PC=2（MC-BN）=4x，
在△PAC中，由余弦定理可得：AC²=PA²+PC²-2PA•PC•cos60°，
即：9=4x²+16x²-2×2x×4x×$\frac{1}{2}$，
解得：x²=$\frac{3}{4}$，
过P作PD⊥AC，垂足为D，则线段PD的长为塔到直路的距离，
∵sin∠BAN=x，cos∠BAN=$\sqrt{1-{x}^{2}}$，
∴sin∠CAP=sin（150°-∠BAN）=$\frac{1}{2}$$\sqrt{1-{x}^{2}}$+$\frac{\sqrt{3}}{2}$x，
∴PD=APsin∠CAP=2x×（$\frac{1}{2}$$\sqrt{1-{x}^{2}}$+$\frac{\sqrt{3}}{2}$x）=x$\sqrt{1-{x}^{2}}$+$\sqrt{3}$x²=$\sqrt{3}$．

点评 本题主要考查了余弦定理在解三角形中的应用，考查了同角三角函数关系式的应用，考查了数形结合思想和计算能力，属于基本知识的考查．