题目内容
(本小题满分15分)设 为数列
为数列 的前
的前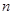 项和,
项和,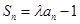 (
( 为常数且
为常数且 ,
, ).
).
(Ⅰ)若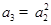 ,求
,求 的值;
的值;
(Ⅱ)对于满足(Ⅰ)中的 ,数列
,数列 满足
满足 ,且
,且 .若不等式
.若不等式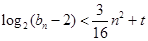 对任意
对任意 恒成立,求实数
恒成立,求实数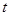 的取值范围.
的取值范围.
 为数列
为数列 的前
的前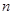 项和,
项和,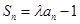 (
( 为常数且
为常数且 ,
, ).
).(Ⅰ)若
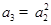 ,求
,求 的值;
的值;(Ⅱ)对于满足(Ⅰ)中的
 ,数列
,数列 满足
满足 ,且
,且 .若不等式
.若不等式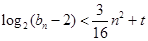 对任意
对任意 恒成立,求实数
恒成立,求实数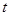 的取值范围.
的取值范围.(Ⅰ)因为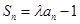 ,
,
所以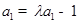 ,
,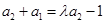 ,
,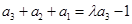 .………4分
.………4分
由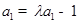 可知:
可知: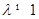 .
.
所以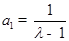 ,
, ,
,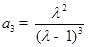 .
.
因为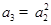 , 所以
, 所以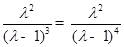 .
.
所以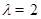 . ……7分
. ……7分
(Ⅱ)因为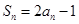 , 所以
, 所以 .
.
所以 ,即
,即 .…………9分
.…………9分
因为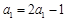 ,即
,即 . 可得:
. 可得: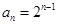 . ………10分
. ………10分
因为 ,且
,且 ,
,
所以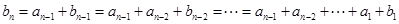
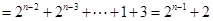 . ……………12分
. ……………12分
因为不等式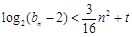 对任意
对任意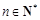 恒成立,
恒成立,
所以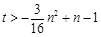 对任意
对任意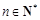 恒成立. ……………13分
恒成立. ……………13分
因为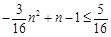 ,且
,且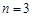 时,
时,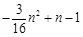 取得最大值
取得最大值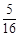 ,
,
所以 . 所以
. 所以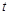 的取值范围是
的取值范围是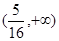 . ………15分
. ………15分
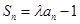 ,
,所以
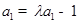 ,
,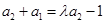 ,
,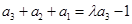 .………4分
.………4分由
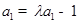 可知:
可知: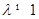 .
. 所以
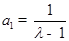 ,
, ,
,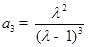 .
.因为
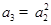 , 所以
, 所以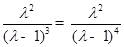 .
.所以
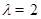 . ……7分
. ……7分(Ⅱ)因为
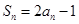 , 所以
, 所以 .
. 所以
 ,即
,即 .…………9分
.…………9分因为
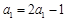 ,即
,即 . 可得:
. 可得: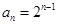 . ………10分
. ………10分因为
 ,且
,且 ,
,所以
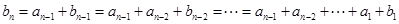
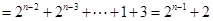 . ……………12分
. ……………12分因为不等式
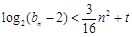 对任意
对任意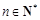 恒成立,
恒成立,所以
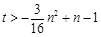 对任意
对任意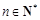 恒成立. ……………13分
恒成立. ……………13分因为
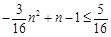 ,且
,且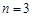 时,
时,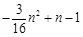 取得最大值
取得最大值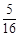 ,
, 所以
 . 所以
. 所以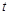 的取值范围是
的取值范围是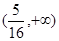 . ………15分
. ………15分(1)先求出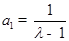 ,进而求出
,进而求出 ,
,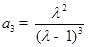 ,再根据
,再根据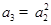 ,建立关于
,建立关于 的方程求解即可.
的方程求解即可.
(II)在(I)的基础上,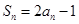 ,然后根据此式,可求得
,然后根据此式,可求得 ,从而求出
,从而求出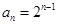 ,
,
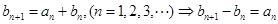 采用叠加的方法求得
采用叠加的方法求得 ,
,
从而把不等式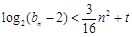 对任意
对任意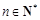 恒成立转化为
恒成立转化为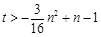 对任意
对任意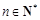 恒成立的常规问题解决.
恒成立的常规问题解决.
解:(Ⅰ)因为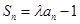 ,
,
所以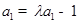 ,
,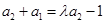 ,
,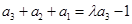 .………4分
.………4分
由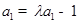 可知:
可知: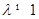 .
.
所以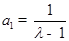 ,
, ,
,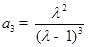 .
.
因为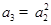 , 所以
, 所以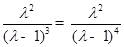 .
.
所以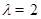 . ……7分
. ……7分
(Ⅱ)因为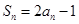 , 所以
, 所以 .
.
所以 ,即
,即 .…………9分
.…………9分
因为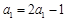 ,即
,即 . 可得:
. 可得: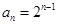 . ………10分
. ………10分
因为 ,且
,且 ,
,
所以
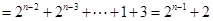 . ……………12分
. ……………12分
因为不等式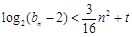 对任意
对任意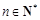 恒成立,
恒成立,
所以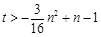 对任意
对任意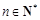 恒成立. ……………13分
恒成立. ……………13分
因为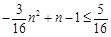 ,且
,且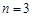 时,
时,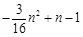 取得最大值
取得最大值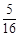 ,
,
所以 . 所以
. 所以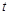 的取值范围是
的取值范围是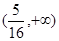 . ………15分
. ………15分
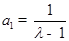 ,进而求出
,进而求出 ,
,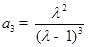 ,再根据
,再根据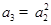 ,建立关于
,建立关于 的方程求解即可.
的方程求解即可.(II)在(I)的基础上,
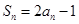 ,然后根据此式,可求得
,然后根据此式,可求得 ,从而求出
,从而求出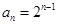 ,
,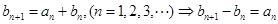 采用叠加的方法求得
采用叠加的方法求得 ,
,从而把不等式
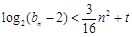 对任意
对任意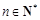 恒成立转化为
恒成立转化为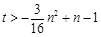 对任意
对任意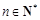 恒成立的常规问题解决.
恒成立的常规问题解决.解:(Ⅰ)因为
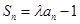 ,
,所以
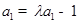 ,
,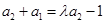 ,
,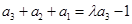 .………4分
.………4分由
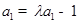 可知:
可知: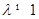 .
. 所以
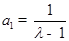 ,
, ,
,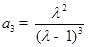 .
.因为
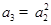 , 所以
, 所以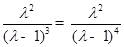 .
.所以
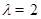 . ……7分
. ……7分(Ⅱ)因为
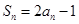 , 所以
, 所以 .
. 所以
 ,即
,即 .…………9分
.…………9分因为
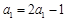 ,即
,即 . 可得:
. 可得: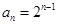 . ………10分
. ………10分因为
 ,且
,且 ,
,所以

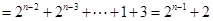 . ……………12分
. ……………12分因为不等式
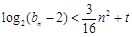 对任意
对任意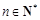 恒成立,
恒成立,所以
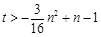 对任意
对任意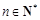 恒成立. ……………13分
恒成立. ……………13分因为
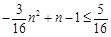 ,且
,且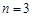 时,
时,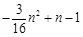 取得最大值
取得最大值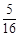 ,
, 所以
 . 所以
. 所以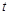 的取值范围是
的取值范围是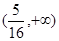 . ………15分
. ………15分
练习册系列答案
相关题目
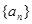 满足
满足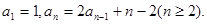 (I)求数列
(I)求数列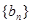 中
中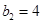 ,前
,前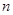 项和为
项和为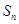 ,且
,且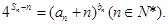 证明:
证明: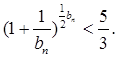
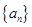 的前
的前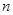 项和为
项和为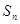 ,等比数列
,等比数列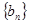 的前
的前 已知数列
已知数列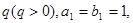

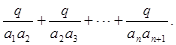
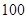 万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过
万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过 年后该项目的资金为
年后该项目的资金为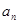 万元.
万元.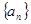 的前三项
的前三项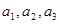 ,并猜想写出通项
,并猜想写出通项 千万元.
千万元.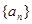 为等差数列,且
为等差数列,且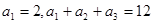 .
.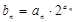 ,求数列
,求数列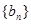 的前
的前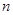 项和
项和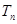 .
.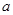 、
、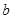 、
、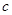 成等差数列,则
成等差数列,则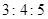 ;
; 的三内角
的三内角 、
、 、
、 成等差数列,则
成等差数列,则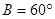 ;
;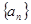 的前
的前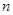 项和为
项和为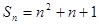 ,则
,则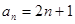 ;
;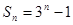 ,则
,则 中,
中,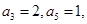 如果数列
如果数列 是等差数列,则
是等差数列,则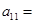 ( )
( )
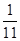
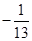

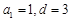 确定的等差数列
确定的等差数列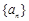 ,当
,当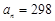 时序号
时序号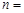 ( )
( ) 中,如果存在正整数
中,如果存在正整数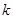 和
和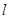 (
(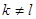 ),使得前
),使得前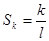 ,前
,前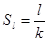 ,则( )
,则( )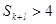
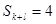
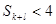
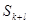 与4的大小关系不确定
与4的大小关系不确定