题目内容
(本小题满分15分)
设等差数列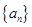 的前
的前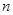 项和为
项和为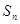 ,等比数列
,等比数列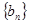 的前
的前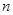 项和为
项和为 已知数列
已知数列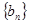 的公比为
的公比为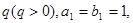

(1)求数列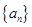 ,
,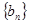 的通项公式;
的通项公式;
(2)求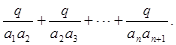
设等差数列
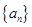 的前
的前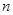 项和为
项和为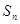 ,等比数列
,等比数列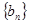 的前
的前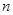 项和为
项和为 已知数列
已知数列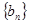 的公比为
的公比为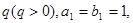

(1)求数列
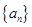 ,
,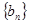 的通项公式;
的通项公式;(2)求
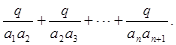
(1)
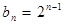
(2)

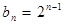
(2)

(1)利用等差和等比数列的定义和性质列出关于数列的参数,进一步求出数列的通项公式;(2)根据数列通项选择裂项求和思想求出数列的前n项和
解:(1)设 的公差为
的公差为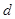 ,则
,则 .解得
.解得 ,所以
,所以 .
.
由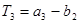 ,得
,得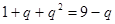 ,又
,又 ,从而解得
,从而解得 ,所以
,所以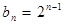 .
.
(2) .
.
所以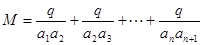 =
=
=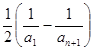 =
=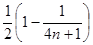 =
= .
.
解:(1)设
 的公差为
的公差为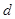 ,则
,则 .解得
.解得 ,所以
,所以 .
.由
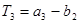 ,得
,得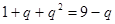 ,又
,又 ,从而解得
,从而解得 ,所以
,所以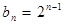 .
. (2)
 .
. 所以
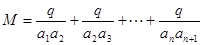 =
=
=
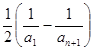 =
=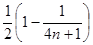 =
= .
.
练习册系列答案
相关题目
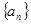 的前
的前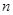 项和为
项和为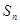 ,且
,且 .
.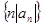 的前
的前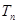 ,求数列
,求数列 的通项公式.
的通项公式.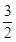 ,bn+1=-
,bn+1=-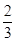 Sn(n∈N*).
Sn(n∈N*).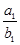 +
+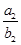 +…+
+…+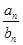 ,求Tn的表达式
,求Tn的表达式 的前
的前 项和为
项和为 ,已知
,已知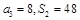 ,数列
,数列 满足
满足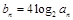 .
. ,使得
,使得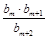 是数列
是数列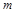 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.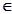 N*,均有S n>0
N*,均有S n>0 为数列
为数列 的前
的前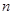 项和,
项和,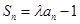 (
( 为常数且
为常数且 ,
, ).
).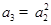 ,求
,求 满足
满足 ,且
,且 .若不等式
.若不等式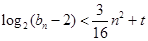 对任意
对任意 恒成立,求实数
恒成立,求实数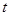 的取值范围.
的取值范围.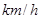 ,这个车队当天一共行驶了多少千米?
,这个车队当天一共行驶了多少千米? 中,
中, ,前
,前 项和为
项和为 ,则
,则 = .
= .  中,前
中,前 项和
项和 ,则
,则 ▲ .
▲ .