题目内容
设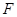 为抛物线
为抛物线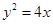 的焦点,
的焦点,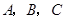 为该抛物线上三点,若
为该抛物线上三点,若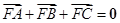 ,则
,则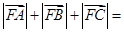 ( )
( )
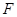 为抛物线
为抛物线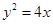 的焦点,
的焦点,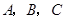 为该抛物线上三点,若
为该抛物线上三点,若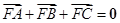 ,则
,则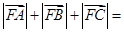 ( )
( )| A.9 | B.6 | C.4 | D.3 |
B
由抛物线方程知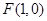 ,
,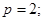 设
设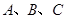 三点的横坐标分别为
三点的横坐标分别为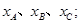 由条件知
由条件知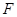 是
是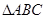 的重心。所以
的重心。所以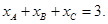 根据抛物线定义得:
根据抛物线定义得:
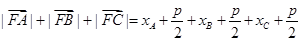
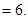 故选B
故选B
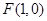 ,
,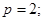 设
设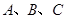 三点的横坐标分别为
三点的横坐标分别为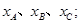 由条件知
由条件知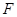 是
是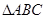 的重心。所以
的重心。所以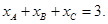 根据抛物线定义得:
根据抛物线定义得: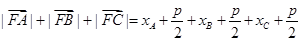
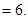 故选B
故选B
练习册系列答案
相关题目
题目内容
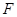 为抛物线
为抛物线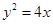 的焦点,
的焦点,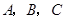 为该抛物线上三点,若
为该抛物线上三点,若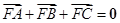 ,则
,则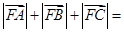 ( )
( )| A.9 | B.6 | C.4 | D.3 |
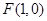 ,
,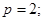 设
设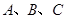 三点的横坐标分别为
三点的横坐标分别为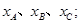 由条件知
由条件知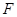 是
是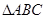 的重心。所以
的重心。所以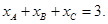 根据抛物线定义得:
根据抛物线定义得: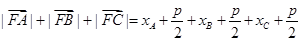
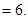 故选B
故选B