题目内容
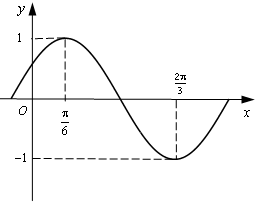
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<
)部分图象如图所示.
(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)设g(x)=f(x)-cos2x,求函数g(x)在区间x∈[0,
]上的最大值和最小值.
| π |
| 2 |
(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)设g(x)=f(x)-cos2x,求函数g(x)在区间x∈[0,
| π |
| 2 |

(Ⅰ)由图可得A=1,
=
-
=
,所以T=π.(2分)
所以ω=2.
当x=
时,f(x)=1,可得sin(2•
+φ)=1,
因为|φ|<
,所以φ=
.(5分)
所以f(x)的解析式为f(x)=sin(2x+
).(6分)
(Ⅱ)g(x)=f(x)-cos2x=sin(2x+
)-cos2x
=sin2xcos
+cos2xsin
-cos2x
=
sin2x-
cos2x=sin(2x-
).(10分)
因为0≤x≤
,所以-
≤2x-
≤
.
当2x-
=
,即x=
时,g(x)有最大值,最大值为1;
当2x-
=-
,即x=0时,g(x)有最小值,最小值为-
.(13分)
| T |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
所以ω=2.
当x=
| π |
| 6 |
| π |
| 6 |
因为|φ|<
| π |
| 2 |
| π |
| 6 |
所以f(x)的解析式为f(x)=sin(2x+
| π |
| 6 |
(Ⅱ)g(x)=f(x)-cos2x=sin(2x+
| π |
| 6 |
=sin2xcos
| π |
| 6 |
| π |
| 6 |
=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
因为0≤x≤
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
当2x-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |

练习册系列答案
相关题目


 +
+ =4则sin2
=4则sin2